問題文全文
\(f(x)=e^{-x}\sin{x}\) として\(,\) 曲線 \(K~:~y=f(x)\) と \(x\) 軸の \(x\geqq 0\) の部分との共有点の \(x\) 座標を小さい方から順に \(p_0,~p_1,~p_2,~\cdots ,~p_n, \cdots\) とおき\(,\) 曲線 \(K\) と \(x\) 軸の \(p_{n-1}\leqq x\leqq p_n\) の部分で囲まれる図形の面積を \(S_n~(n\geqq 1)\) とおくとき\(,\) 以下の問いに答えなさい.
(1) \(p_n\) を求めなさい.
(2) \(0\leqq x\leqq 2 \pi\) の範囲で関数 \(f(x)\) の極値と曲線 \(K\) の変曲点を求めなさい.
(3) \(S_1\) を求めなさい.
(4) \(S_n\) を \(S_1\) を用いて表しなさい.
(5) \(\displaystyle \sum_{n=1}^{\infty}S_n\) を求めなさい.
(1) の解答
\begin{align}e^{-x}\sin{x}=0\end{align}
\(e^{-x}>0\) より\(,\)
\begin{align}\sin{x}=0\end{align}
\begin{align}x=n\pi~(n\geqq 0)\end{align}
\begin{align}p_n=n\pi~(n\geqq 0)~~~~\cdots \fbox{答}\end{align}
(2) の解答
\begin{align}f^{\prime}(x)=-e^{-x}\sin{x}+e^{-x}\cos{x}\end{align}
\begin{align}=e^{-x}\sin{\left(x+\frac{3}{4}\pi \right)}\end{align}
\(0\leqq x\leqq 2\pi \) より\(,\)
\begin{align}\frac{3}{4}\pi \leqq x+\frac{3}{4}\pi \leqq \frac{11}{4}\pi \end{align}
であるから\(,\) \(f^{\prime}(x)=0\) のとき\(,\)
\begin{align}x+\frac{3}{4}\pi =\pi ,~2\pi \end{align}
\begin{align}x=\frac{\pi}{4},~\frac{5}{4}\pi \end{align}
\begin{align}f^{\prime \prime}(x)=-e^{-x}\sin{\left(x+\frac{3}{4}\pi \right)}+e^{-x}\cos{\left( x+\frac{3}{4}\pi \right)}\end{align}
\begin{align}=e^{-x}\sin{\left(x+\frac{3}{2}\pi \right)}\end{align}
\(0\leqq x\leqq 2\pi \) より\(,\)
\begin{align}\frac{3}{2}\pi \leqq x+\frac{3}{2}\pi \leqq \frac{7}{2}\pi \end{align}
なので\(,\) \(f^{\prime \prime}(x)=0\) のとき\(,\)
\begin{align}x+\frac{3}{2}\pi =2\pi ,~3\pi \end{align}
\begin{align}x=\frac{\pi}{2},~\frac{3}{2}\pi \end{align}
よって\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline x & 0 & \cdots & \displaystyle \frac{\pi}{4} & \cdots & \displaystyle \frac{\pi}{2} & \cdots & \displaystyle \frac{5}{4}\pi & \cdots & \displaystyle \frac{3}{2}\pi & \cdots & 2\pi \\ \hline f^{\prime}(x) & {} & + & 0 & – & – & – & 0 & + & + & + & {} \\ \hline f^{\prime \prime}(x) & {} & – & – & – & 0 & + & + & + & 0 & – & {} \\ \hline f(x) & 0 & \nearrow \cap & \displaystyle \frac{1}{\sqrt{2}e^{\frac{\pi}{4}}} & \searrow \cap & e^{-\frac{\pi}{2}} & \searrow \cup & \displaystyle \frac{1}{\sqrt{2}e^{\frac{5}{4}\pi}} & \nearrow \cup & -e^{-\frac{3}{2}\pi} & \nearrow \cap & 0 \\ \hline \end{array}\end{align}
増減表より\(,\)
\begin{align}x=\frac{\pi}{4}~のとき~~極大値 ~\frac{1}{\sqrt{2}e^{\frac{\pi}{4}}}~~~~\cdots \fbox{答}\end{align}
\begin{align}x=\frac{5}{4}\pi ~のとき~~極小値~-\frac{1}{\sqrt{2}e^{\frac{5}{4}\pi}}~~~~\cdots \fbox{答}\end{align}
\begin{align}変曲点~~\left(\frac{\pi}{2},~e^{-\frac{\pi}{2}}\right),~\left(\frac{3}{2}\pi ,~-e^{-\frac{3}{2}\pi}\right) ~~~~\cdots \fbox{答}\end{align}
(3) の解答
(1) で求めた \(x\) 切片と (2) の増減表から\(,\) \(y=f(x)\) のグラフは下図のようになる.
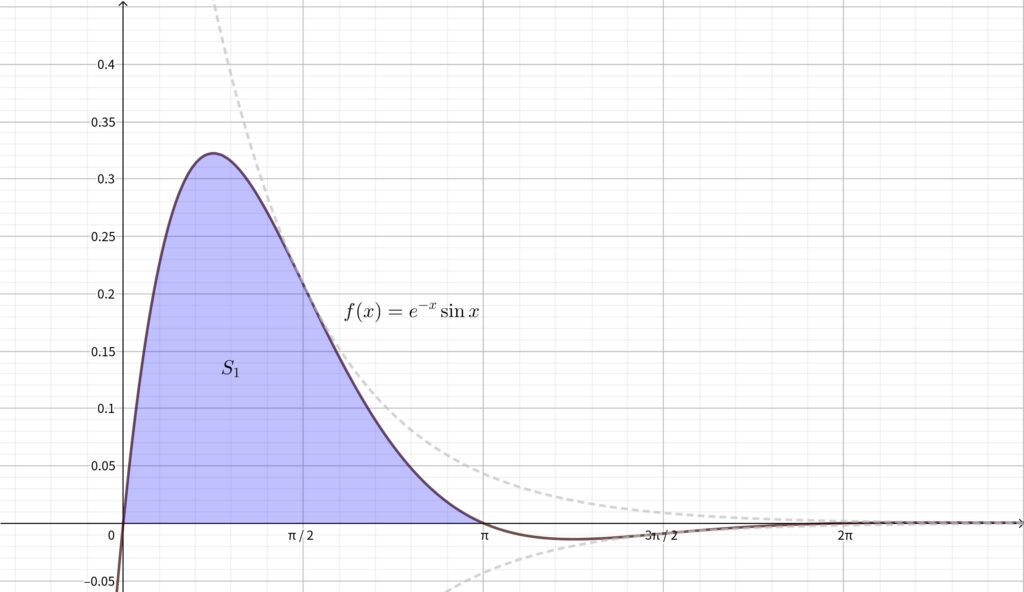
\begin{align}S_1=\int_0^{\pi}e^{-x}\sin{x}dx\end{align}
\begin{align}=\biggl[e^{-x}(-\cos{x})\biggr]_0^{\pi}-\int_0^{\pi}-e^{-x}(-\cos{x})dx\end{align}
\begin{align}=e^{-\pi}+1-\int_0^{\pi}e^{-x}\cos{x}dx\end{align}
\begin{align}=e^{-\pi}+1-\left(\biggl[e^{-x}\sin{x}\biggr]_0^{\pi}-\int_0^{\pi}-e^{-x}\sin{x}dx\right)\end{align}
\begin{align}=e^{-\pi}+1-S_1\end{align}
\begin{align}2S_1=e^{-\pi}+1\end{align}
\begin{align}S_1=\frac{e^{-\pi}+1}{2}~~~~\cdots \fbox{答}\end{align}
(4) の着眼点
「\(S_n\) を \(S_1\) で表せ.」
と言われています.
\(S_n\) の定義域は \((n-1)\pi \leqq x\leqq n\pi\) です. これを \(S_1\) で表すということは\(,\) その定義域が \(0\leqq x\leqq \pi\) となってくれればいいのではないかと考えます.
経験がないとなかなか思いつかないかもしれませんが\(,\)
\begin{align}t=x-(n-1)\pi\end{align}
とおくことでうまく定義域を変更できます.
(4) の解答
\begin{align}S_n=\left|\int_{(n-1)\pi}^{n\pi}e^{-x}\sin{x}dx\right|\end{align}
\(t=x-(n-1)\pi\) とおくと\(,\) \(dt=dx\) であり\(,\)
\begin{align}\begin{array}{c|ccc}x & (n-1)\pi & \to & n\pi \\ \hline t & 0 & \to & \pi\end{array}\end{align}
であるから\(,\)
\begin{align}S_n=\left|\int_0^{\pi}e^{-\{t+(n-1)\pi\}}\sin{\{t+(n-1)\pi\}}dt\right|\end{align}
\begin{align}=\left|e^{-(n-1)\pi}\int_0^{\pi}e^{-t}\cdot (-1)^{n-1}\sin{t}dt\right|\end{align}
\begin{align}=\left|e^{-(n-1)\pi}\right|\left|(-1)^{n-1}\right|\left|\int_0^{\pi}e^{-t}\sin{t}dt\right|\end{align}
\(e^{-(n-1)\pi}>0\)\(,\) \(|(-1)^{n-1}|=1\)\(,\) \(S_1>0\) より\(,\)
\begin{align}S_n=e^{-(n-1)\pi}S_1~~~~\cdots \fbox{答}\end{align}
(5) の解答
初項 \(S_1\)\(,\) 公比 \(e^{-\pi}\) の無限等比級数の和であるから\(,\)
\begin{align}\sum_{n=1}^{\infty}S_n=\frac{1}{1-e^{-\pi}}S_1\end{align}
\begin{align}=\frac{e^{\pi}}{e^{\pi}-1}\cdot \frac{e^{-\pi}+1}{2}=\frac{1+e^{\pi}}{2(e^{\pi}-1)}~~~~\cdots \fbox{答}\end{align}

quandle
初項 \(a\)\(,\) 公比 \(r~(|r|<1)\) の無限等比級数の和は
\begin{align}\frac{a}{1-r}\end{align}
でしたね.






コメント