問題文全文 原点を \(\mathrm{O}\) とする座標平面において \(3\) 点 \(\displaystyle \mathrm{A}(-3,~0),~\mathrm{B}(0,~1),~\mathrm{C}\left(-1,~\frac{1}{2}\right)\) をとる. \(t\) を \(0\leqq t \leqq 1\) をみたす実数とする. \(\mathrm{P}\) を \(\mathrm{AP}=t\mathrm{AC}\) をみたす線分 \(\mathrm{AC}\) 上の点\(,\) \(\mathrm{Q}\) を \(\mathrm{CQ}=t\mathrm{CB}\) をみたす線分 \(\mathrm{CB}\) 上の点\(,\) \(\mathrm{R}\) を \(\mathrm{PR}=t\mathrm{PQ}\) をみたす線分 \(\mathrm{PQ}\) 上の点とする. \(t\) が \(0\leqq t \leqq 1\) の範囲を動くときの \(\mathrm{R}\) の軌跡を \(\ell_1\) とする.
(1) \(\ell_1\) の方程式は
\begin{align}x=-~\fbox{$\hskip0.8emさ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~y^2+~\fbox{$\hskip0.8emし\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~y-~\fbox{$\hskip0.8emす\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~,~\fbox{$\hskip0.8emせ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~\leqq y \leqq \fbox{$\hskip0.8emそ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
と表され\(,\) \(x\) 軸と \(y\) 軸と \(\ell_1\) で囲まれる部分の面積は \(\displaystyle \frac{\fbox{$\hskip0.8emた\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emち\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) である.
(2) \(\ell_1\) 上の点 \((a,~b)\) における \(\ell_1\) の接線 \(\ell_2\) の方程式は \(b\) を用いて
\begin{align}x=(-~\fbox{$\hskip0.8emつ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~b+~\fbox{$\hskip0.8emて\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~)y+~\fbox{$\hskip0.8emと\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~b^2-~\fbox{$\hskip0.8emな\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
とかける.
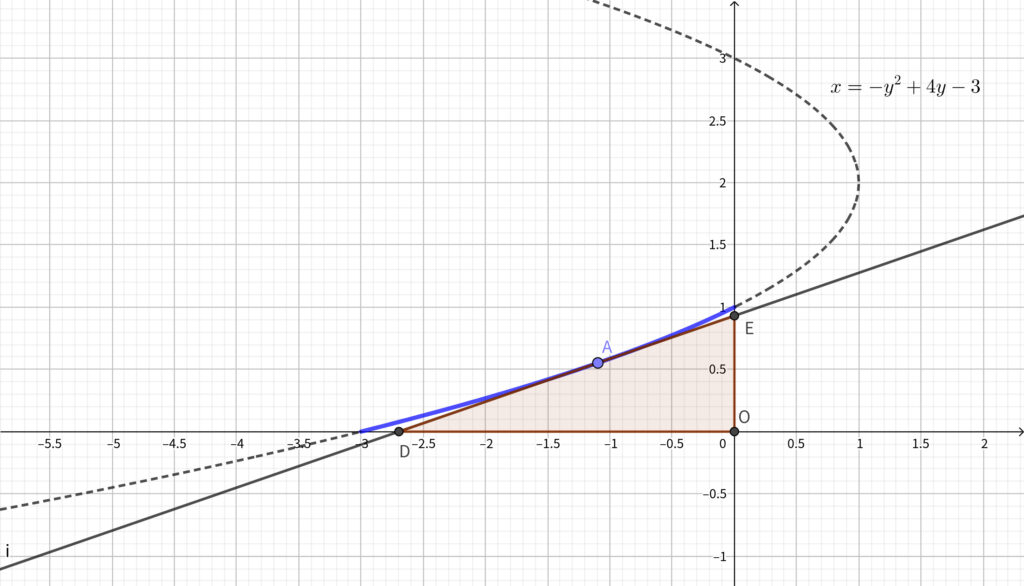
\(\ell_2\) と \(x\) 軸との交点を \(\mathrm{D}\)\(,\) \(\ell_2\) と \(y\) 軸との交点を \(\mathrm{E}\) とする. \(b\) が \(0\leqq b \leqq 1\) の範囲を動くとき\(,\) 三角形 \(\mathrm{ODE}\) の面積は
\begin{align} b=\frac{\fbox{$\hskip0.8emに\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emぬ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-~\frac{\fbox{$\hskip0.8emね\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emの\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~\sqrt{\fbox{$\hskip0.8emは\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
のとき最大値
\begin{align}\frac{\fbox{$\hskip0.8emひふ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emへほ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~\sqrt{\fbox{$\hskip0.8emま\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-~\frac{\fbox{$\hskip0.8emみむ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emめも\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
をとる.
軌跡を求める手順 \(\mathrm{R}\) の軌跡 \(\ell_1\) を求める問題です. 軌跡は以下の \(3\) ステップで解けます.
(1) の問題もこの手順で解くことができます. 問題文はベクトルで与えられていませんが\(,\) ベクトル方程式で表すことで楽に処理ができます. 軌跡を表したいときはベクトル方程式が強力な武器になりますので積極的に利用しましょう.
(1) の解答
\begin{align}\overrightarrow{\mathrm{AP}}=t\overrightarrow{\mathrm{AC}}=\left(2t,~\frac{1}{2}t\right)\end{align}
\begin{align}\overrightarrow{\mathrm{CQ}}=r\overrightarrow{\mathrm{CB}}=\left(t,~\frac{1}{2}t\right)\end{align}
\begin{align}\overrightarrow{\mathrm{AQ}}=\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CQ}}=\left(2+t,~\frac{1}{2}+\frac{1}{2}t\right)\end{align}
\begin{align}\overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{AQ}}-\overrightarrow{\mathrm{AP}}=\left(2-t,~\frac{1}{2}\right)\end{align}
\begin{align}\overrightarrow{\mathrm{PR}}=t\overrightarrow{\mathrm{PQ}}=\left(2t-t^2,~\frac{1}{2}t\right)\end{align}
\begin{align}\overrightarrow{\mathrm{OR}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AP}}+\overrightarrow{\mathrm{PR}}\end{align}
\begin{align}=\left(-3+2t+(2t-t^2),~0+\frac{1}{2}t+\frac{1}{2}t\right)=(-t^2+4t-3,~t)\end{align}
\(\mathrm{R}(x,~y)\) とおくと\(,\)
\begin{align}\left\{\begin{array}{c}x=-t^2+4t-3 \\ y=t\end{array}\right.\end{align}
\(0\leqq t\leqq 1\) より\(,\) \(0\leqq y\leqq 1\) であり\(,\) \(t\) を消去すると以下を得る.
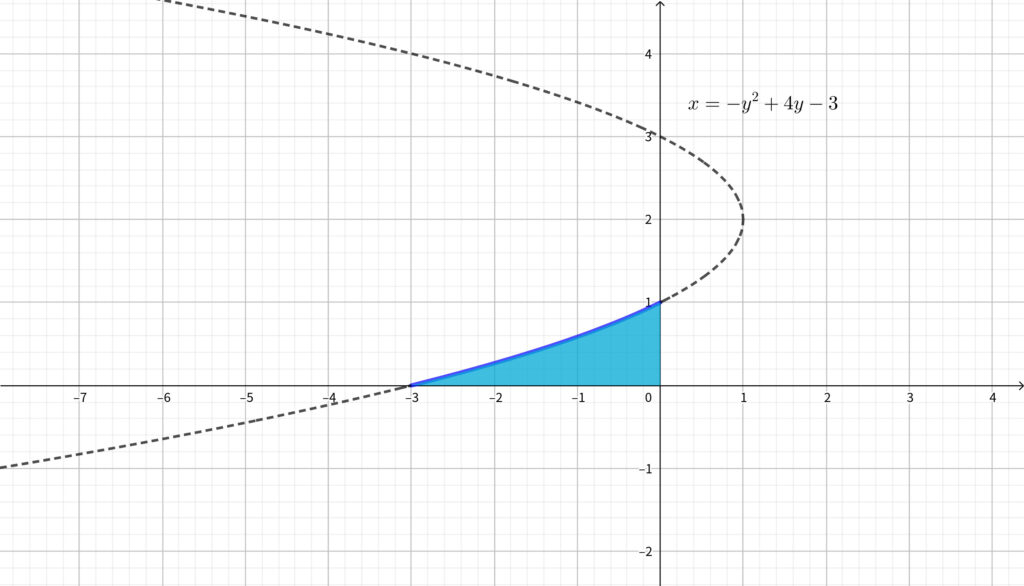
\begin{align}x=-y^2+4y-3~~(0\leqq y\leqq 1)~~~~\cdots \fbox{答}\end{align}
求める面積 \(S\) は上図の青色部分であるから\(,\)
\begin{align}S=\int_{-3}^0ydx\end{align}
で求められる. \(dx=(-2y+4)dy\) であり\(,\)
\begin{align}\begin{array}{|c|ccc|}\hline x & -3 & \to & 0 \\ \hline y & 0 & \to & 1 \\ \hline \end{array}\end{align}
であるから\(,\)
\begin{align}S=\int_0^1 y(-2y+4)dy\end{align}
\begin{align}=\biggl[-\frac{2}{3}y^3+2y^2\biggr]_0^1=\frac{4}{3}~~~~\cdots \fbox{答}\end{align}
さ:1 し:4 す:3 せ:0 そ:1 た:4 ち:3
面積の別解
\begin{align}S=\int_0^1-xdy\end{align}
\begin{align}=\int_0^1(y^2-4y+3)dy=\biggl[\frac{1}{3}y^3-2y^2+3y\biggr]_0^1\end{align}
\begin{align}=\frac{1}{3}-2+3=\frac{4}{3}~~~~\cdots \fbox{答}\end{align}
quandle
求めたい面積は \(x\) 軸に関して負の部分にありますから\(,\) 被積分関数にマイナスをつけ忘れないようにしよう.
(2) の解答
\begin{align}\frac{dx}{dy}=-2y+4\end{align}
より\(,\)
\begin{align}\frac{dy}{dx}=\frac{1}{-2y+4}\end{align}
\begin{align}\ell_2 ~:~y=\frac{1}{-2b+4}(x-a)+b\end{align}
\begin{align}(-2b+4)y=x-a+b(-2b+4)\end{align}
\begin{align}x=(-2b+4)y+a-b(-2b+4)\end{align}
\(a=-b^2+4b-3\) より\(,\)
\begin{align}x=(-2b+4)y+b^2-3~~~~\cdots \fbox{答}\end{align}
\(x=0\) のとき \(\displaystyle y=\frac{b^2-3}{2b-4}\) であるから
\begin{align}\mathrm{E}\left(0,~\frac{b^2-3}{2b-4}\right)\end{align}
\(y=0\) のとき \(\displaystyle x=b^2-3\) であるから
\begin{align}\mathrm{D}(b^2-3,~0)\end{align}
\(0\leqq b \leqq 1\) のとき
\begin{align}b^2-3<0,~\frac{b^2-3}{2b-4}>0\end{align}
であるから\(,\)
\begin{align}\mathrm{OD}=3-b^2,~\mathrm{OE}=\frac{b^2-3}{2b-4}\end{align}
\begin{align}\triangle \mathrm{ODE}=\frac{1}{2}\cdot \mathrm{OD}\cdot \mathrm{OE}\end{align}
\begin{align}=\frac{1}{2}\cdot (3-b^2)\cdot \frac{b^2-3}{2b-4}=\frac{1}{4}\cdot \frac{(3-b^2)^2}{2-b}\end{align}
\begin{align}f(b)=\frac{(3-b^2)^2}{2-b}~~(0\leqq b \leqq 1)\end{align}
とおく.
\begin{align}f^{\prime}(b)=\frac{2(3-b^2)(-2b)-(3-b^2)^2(-1)}{(2-b)^2}\end{align}
\begin{align}=\frac{(3-b^2)(3b^2-8b+3)}{(2-b)^2}\end{align}
\(0\leqq b \leqq 1\) より\(,\) \(\displaystyle \frac{3-b^2}{(2-b)^2}>0\) なので\(,\) \(f^{\prime}(b)\) の符号と \(3b^2-8b+3\) の符号は一致する.
\(3b^2-8b+3=0\) のとき\(,\)
\begin{align}b=\frac{4\pm \sqrt{16-9}}{3}=\frac{4\pm \sqrt{7}}{3}\end{align}
であるから\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline b & 0 & \cdots & \displaystyle \frac{4-\sqrt{7}}{3} & \cdots & 1 \\ \hline f^{\prime}(b) & {} & + & 0 & – & {} \\ \hline f(b) & {} & \nearrow & 極大 & \searrow & {} \\ \hline \end{array}\end{align}
増減表より\(,\) 最大値をとる \(b\) の値は
\begin{align}b=\frac{4}{3}-\frac{1}{3}\sqrt{7}~~~~\cdots \fbox{答}\end{align}
である. ここで\(,\) \(3b^2-8b+3=0\) より\(,\)
\begin{align}b^2=\frac{8}{3}b-1\end{align}
\begin{align}3-b^2=4-\frac{8}{3}b\end{align}
\begin{align}=4-\frac{8}{3}\cdot \frac{4-\sqrt{7}}{3}=\frac{4+8\sqrt{7}}{9}\end{align}
\begin{align}2-b=2-\frac{4-\sqrt{7}}{3}=\frac{2+\sqrt{7}}{3}\end{align}
であるから\(,\) 最大値は
\begin{align}f\left(\frac{4-\sqrt{7}}{3}\right)=\left(\frac{4+8\sqrt{7}}{9}\right)^2\cdot \frac{3}{2+\sqrt{7}}\end{align}
\begin{align}=\frac{16(1+2\sqrt{7})^2}{27(2+\sqrt{7})}=\frac{16(29+4\sqrt{7})(\sqrt{7}-2)}{81}\end{align}
\begin{align}=\frac{16(21\sqrt{7}-30)}{81}=\frac{4(7\sqrt{7}-10)}{27}\end{align}
\begin{align}=\frac{28}{27}\sqrt{7}-\frac{40}{27}~~~~\cdots \fbox{答}\end{align}
quandle
最大値を計算するときにあらかじめ
\(3-b^2\) と \(2-b\) をつくっておくと代入しやすくなります.
に:4 ぬ:3 ね:1 の:3 は:7 ひ:2 ふ:8





コメント