公立諏訪前期2021年第1問の問題文全文
\(3\) 次関数 \(f(x)=x^3+3x^2\) は\(,\) \(x=a\) で極大になる. 点 \((a,~f(a))\) を \(\mathrm{P}\) とし\(,\) \(m=f(a)\) とおく. このとき\(,\) 以下の問いに答えなさい.
(1) \(\mathrm{P}\) の座標を求めなさい.
(2) 曲線 \(y=f(x)\) と直線 \(y=m\) の共有点のうち\(,\) \(\mathrm{P}\) 以外の点 \(\mathrm{A}\) の座標を求めなさい.
(3) 曲線 \(y=f(x)\) 上の点 \(\mathrm{B}(b,~f(b))\) を通り\(,\) 曲線 \(y=f(x)\) 上の別の点で接する接線の方程式を求めなさい. ただし\(,\) \(0\leqq b <1\) とする.
(4) (3) で求めた接線と直線 \(y=m\) の交点 \(\mathrm{C}\) の座標を求めなさい.
(5) \(\triangle \mathrm{ABC}\) の面積を求めなさい.
(1) の解答〜極大をとることの確認は必須〜
\begin{align}f^{\prime}(x)=3x^2+6x=3x(x+2)\end{align}
であるから\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline x & \cdots & -2 & \cdots & 0 & \cdots \\ \hline f^{\prime}(x) & + & 0 & – & 0 & \cdots \\ \hline f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\ \hline \end{array}\end{align}
増減表より\(,\) \(x=-2\) のときに極大値をとるので\(,\)
\begin{align}a=-2\end{align}
このとき\(,\)
\begin{align}f(-2)=-8+3\cdot 4=4\end{align}
であるから\(,\) 求める点 \(\mathrm{P}\) の座標は
\begin{align}\mathrm{P}(-2,~4)~~~~\cdots \fbox{答}\end{align}
(2) の解答〜グラフを見て因数分解する〜
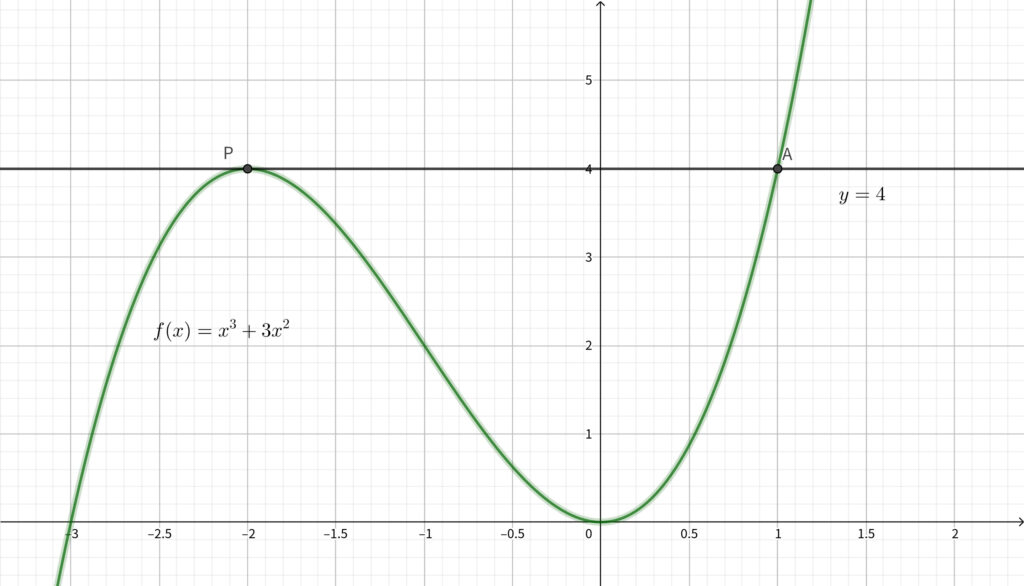
(1) より\(,\)
\begin{align}m=4\end{align}
\begin{align}x^3+3x^2=4\end{align}
のとき\(,\)
\begin{align}x^3+3x^2-4=0\end{align}
\begin{align}(x+2)^2(x-1)=0\end{align}
\begin{align}x=-2,~1\end{align}
\begin{align}\mathrm{A}(1,~4)~~~~\cdots \fbox{答}\end{align}

quandle
\(3\) 次式を因数分解する必要がありますが\(,\) \(y=f(x)\) のグラフと 直線 \(y=4\) は \(x=-2\) で接しているのですから\(,\) \((x+2)^2\) を因数にもつことは確定しています. あとは定数項部分を考えると必然的にもう一つの因数は \((x-1)\) で決まってしまいます.
このように数Ⅱの微積分の問題ではグラフの形から因数分解の形がわかってしまうことが少なくないので\(,\) すぐに因数定理に頼るのではなく\(,\) グラフの形から予測する癖をつけると速く解けるようになります.

quandle
詳細は割愛しますが\(,\) \(4\) 等分定理を知っている方であれば\(,\) グラフを描くだけで \(\mathrm{A}\) の \(x\) 座標が \(1\) になることはすぐに分かります.
(3) の解答〜再度グラフを見て因数分解〜
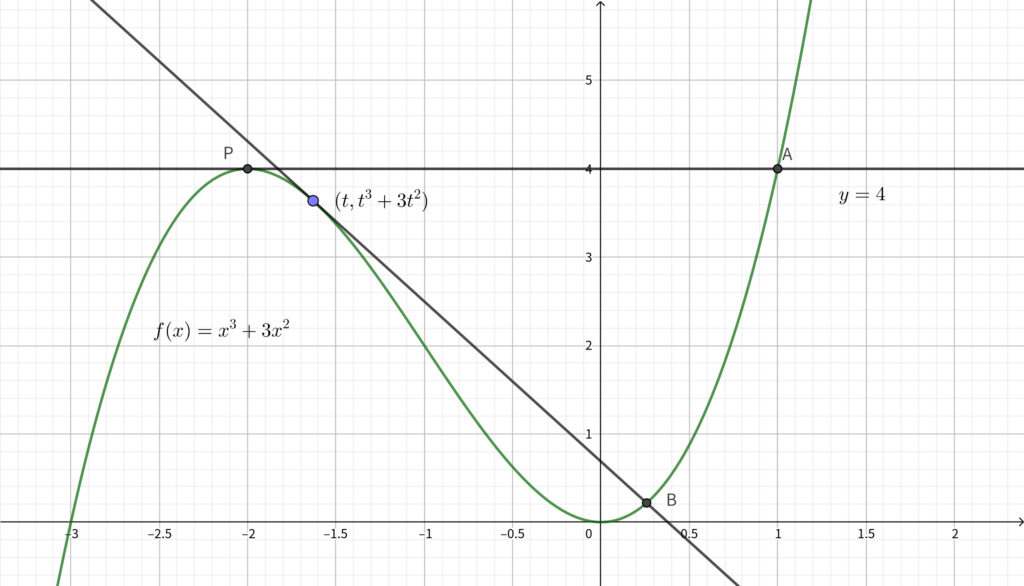
接点を \((t,~t^3+3t^2)\) とおくと\(,\) 接線の方程式は
\begin{align}y=(3t^2+6t)(x-t)+t^3+3t^2\end{align}
\begin{align}y=(3t^2+6t)x-2t^3-3t^2\end{align}
\(y=f(x)\) のグラフと接線の共有点の \(x\) 座標は
\begin{align}x^3+3x^2=(3t^2+6t)(x-t)+t^3+3t^2\end{align}
つまり\(,\)
\begin{align}x^3+3x^2-(3t^2+6t)x+2t^3+3t^2=0\end{align}
の解であり\(,\) \(x=t\) で接することから\(,\) \((x-t)^2\) を因数にもつので\(,\)
\begin{align}(x-t)^2\{x-(-2t-3)\}=0\end{align}
よって\(,\) \(\mathrm{B}\) の \(x\) 座標 \(b\) は
\begin{align}b=-2t-3\end{align}
とかける. つまり\(,\)
\begin{align}t=\frac{-b-3}{2}\end{align}
であるから\(,\) 求める接線の方程式は
\begin{align}y=\left(3\cdot \frac{b^2+6b+9}{4}+6\cdot \frac{-b-3}{2}\right)x-2\cdot \frac{-b^3-9b^2-27b-27}{8}-3\cdot \frac{b^2+6b+9}{4}\end{align}
\begin{align}y=\frac{3b^2+18b+27-12b-36}{4}x+\frac{b^3+9b^2+27b+27-3b^2-18b-27}{4}\end{align}
\begin{align}y=\frac{3b^2+6b-9}{4}x+\frac{b^3+6b^2+9b}{4}~~~~\cdots \fbox{答}\end{align}
(4) の解答
\begin{align}\frac{3b^2+6b-9}{4}x+\frac{b^3+6b^2+9b}{4}=4\end{align}
のとき\(,\)
\begin{align}(3b^2+6b-9)x=-b^3-6b^2-9b+16\end{align}
\begin{align}3(b+3)(b-1)x=-(b-1)(b^2+7b+16)\end{align}
\(0\leqq b <1\) より\(,\) \(b-1\neq 0\) であるから\(,\)
\begin{align}x=\frac{-b^2-7b-16}{3b+9}\end{align}
よって\(,\) \(\mathrm{C}\) の座標は
\begin{align}\mathrm{C}\left(\frac{-b^2-7b-16}{3b+9},~4\right)~~~~\cdots \fbox{答}\end{align}
(5) の着眼点〜底辺は \(\mathrm{AC}\) 〜
三角形の面積を求める問題です. 高校で扱える三角形の公式は様々あるので\(,\) どれを使えばもっとも楽に求まるのかを判断する必要があります.
今回であれば\(,\) 点 \(\mathrm{A}\) と点 \(\mathrm{C}\) の \(y\) 座標がともに \(4\) で等しいので\(,\) \(\mathrm{AC}\) を底辺と見ましょう. 点 \(\mathrm{B}\) から 直線 \(\mathrm{AC}\) に下ろした垂線の足 \(\mathrm{H}\) とおくとき\(,\) 高さは \(\mathrm{BH}\) の長さとなります.
(5) の解答〜大小関係をしっかり調べる〜
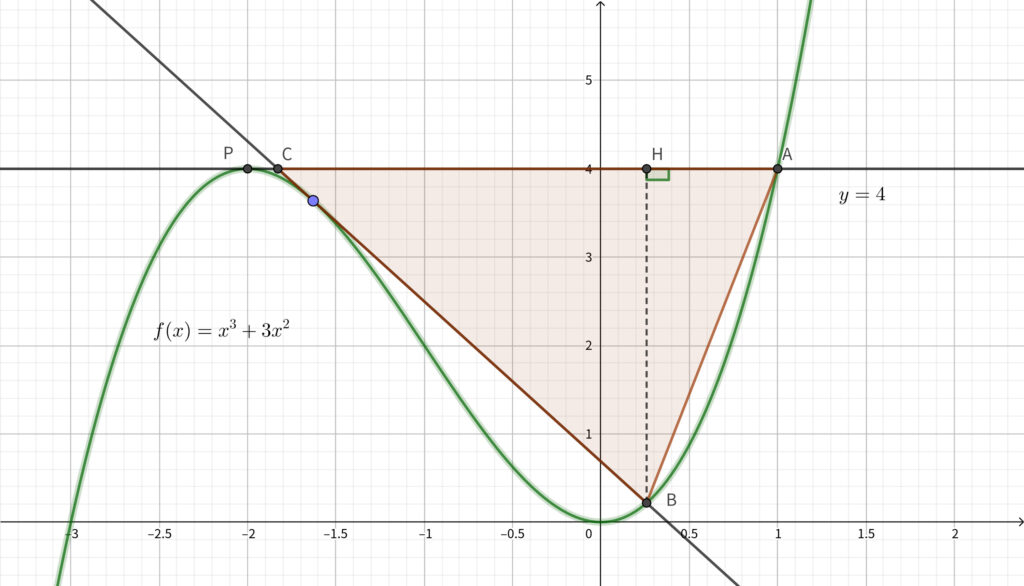
点 \(\mathrm{B}\) から直線 \(\mathrm{AC}\) に下ろした垂線の足を \(\mathrm{H}\) とおく.
\(0\leqq b <1\) より\(,\)
\begin{align}\frac{-b^2-7b-16}{3b+9}<0(<1)\end{align}
\begin{align}b^3+3b^2<1^3+3\cdot 1^2=4\end{align}
であるから\(,\)
\begin{align}\mathrm{AC}=1-\frac{-b^2-7b-16}{3b+9}\end{align}
\begin{align}=\frac{3b+9+b^2+7b+16}{3b+9}=\frac{b^2+10b+25}{3b+9}\end{align}
\begin{align}=\frac{(b+5)^2}{3b+9}\end{align}
\begin{align}\mathrm{BH}= 4-(b^3+3b^2)=(b+2)^2(1-b)\end{align}
よって\(,\) 求める面積は
\begin{align}\triangle \mathrm{ABC}=\frac{1}{2}\cdot \mathrm{AC}\cdot \mathrm{BH}\end{align}
\begin{align}=\frac{1}{2}\cdot \frac{(b+5)^2}{3(b+3)}\cdot (b+2)^2(1-b)\end{align}
\begin{align}=\frac{(b+5)^2(b+2)^2(1-b)}{6(b+3)}~~~~\cdots \fbox{答}\end{align}









コメント