東京理科大学理工学部（数・物・情・応生・経営工）2022年第３問

理工（数・物・情・応生・経営工）
スポンサーリンク

理工学部（数・物・情・応生・経営工）2022年第３問の問題文全文

関数 \(f(x)\) を次で定める.

\begin{align}f(x)=\frac{1}{x}~~(x>0)\end{align}

座標平面上の曲線 \(y=f(x)\) を \(C\) とする. \(C\) 上の点 \(\displaystyle \mathrm{P}\left(2,~\frac{1}{2}\right)\) と\(,\) 正の定数 \(t\) に対して \(y\) 軸上の点 \(\mathrm{A}(0,~-t)\) をとる. 点 \(\mathrm{A}\) と点 \(\mathrm{P}\) を通る直線を \(\ell_1\) とする.

(1) 直線 \(\ell_1\) を表す方程式を\(,\) \(t\) を用いて表せ.

(2) \(C\) 上の点 \(\mathrm{P}\) における \(C\) の法線と \(y\) 軸の交点を \((0,~-t_0)\) とおく. \(t_0\) を求めよ.

上の (2) で求めた \(t_0\) に対して \(t<t_0\) とする. 点 \(\mathrm{P}\) を通り\(,\) 直線 \(\ell_1\) に垂直な直線を \(\ell_2\) とする. \(\ell_2\) と \(C\) の交点のうち\(,\) 点 \(\mathrm{P}\) と異なる点を \(\mathrm{Q}\) とおく.

(3) 点 \(\mathrm{Q}\) の座標を\(,\) \(t\) を用いて表せ.

最後に\(,\) \(\displaystyle t=\frac{3}{2}\) のときを考える.

(4) 点 \(\mathrm{Q}\) を通る \(C\) の接線を \(\ell_3\) とする. このとき\(,\) \(2\) つの直線 \(\ell_1,~\ell_3\) および曲線 \(C\) で囲まれた部分の面積を求めよ.

(1) の解答〜 傾きだけを求める〜

\(\ell_1\) は \(2\) 点 \(\displaystyle \mathrm{A}(0,~-t),~\mathrm{P}\left(2,~\frac{1}{2}\right)\) を通る直線であるから\(,\)

\begin{align}\ell_1~:~y=\cfrac{\cfrac{1}{2}-(-t)}{2-0}x-t\end{align}

\begin{align}\ell_1~:~y=\frac{1+2t}{4}x-t~~~~\cdots \fbox{答}\end{align}

quandle
quandle

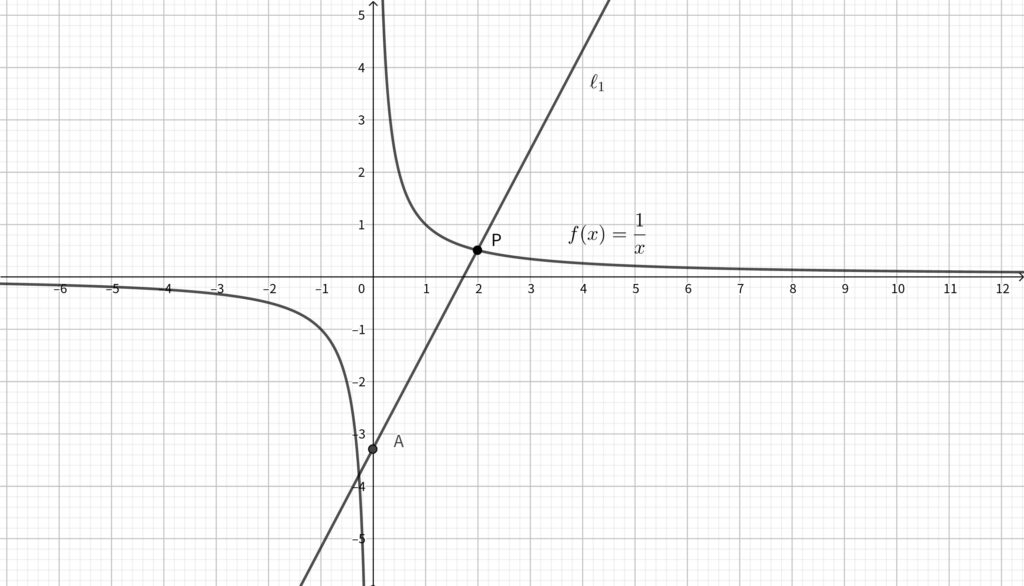
\(\mathrm{A}\) を通ることから\(,\) \(y\) 切片は \(-t\) と分かっているので\(,\) 傾きだけ出せばいいですね.

(2) の解答〜法線の傾きは “マイナス逆数” 〜

\(\displaystyle f^{\prime}(x)=-\frac{1}{x^2}\) より\(,\) \(\displaystyle f^{\prime}(2)=-\frac{1}{4}\)

\(C\) の法線を \(n\) とおくと\(,\) \(n\) の傾きは\(,\) \(\displaystyle -\frac{1}{f^{\prime}(2)}=4\) であるから\(,\)

\begin{align}n~:~y=4(x-2)+\frac{1}{2}\end{align}

\begin{align}n~:~y=4x-\frac{15}{2}\end{align}

\begin{align}t_0=\frac{15}{2}~~~~\cdots \fbox{答}\end{align}

(3) の解答〜\(C\) と \(\ell_2\) の交点の \(x\) 座標の\(1\) つは \(2\)〜

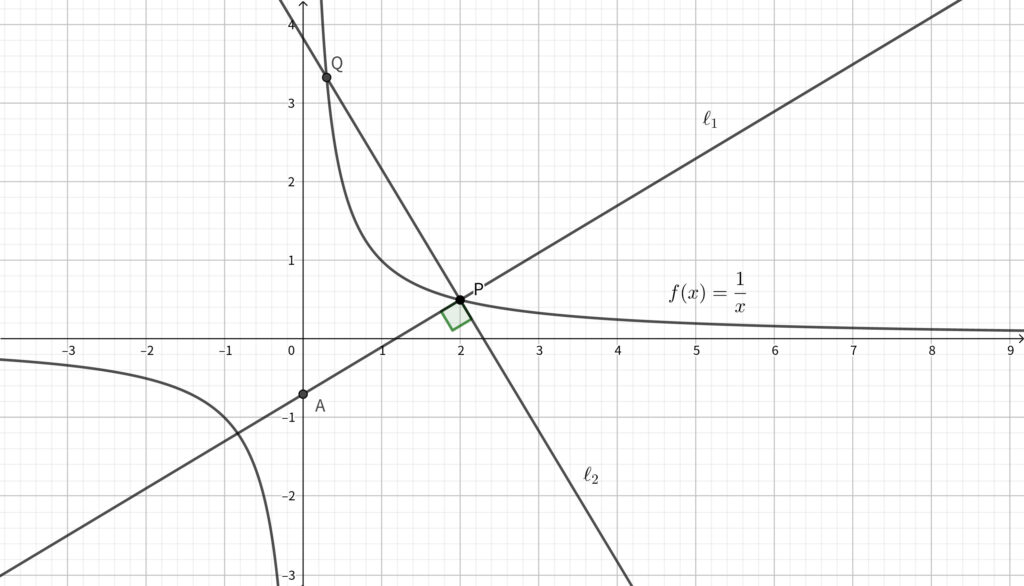
(1) より \(\ell_1\) の傾きは \(\displaystyle \frac{1+2t}{4}\) である.

\(\ell_1 \perp \ell_2\) であることより\(,\) \(\ell_2\) の傾きは \(\displaystyle -\frac{4}{1+2t}\) であるから\(,\)

\begin{align}\ell_2~:~y=-\frac{4}{1+2t}(x-2)+\frac{1}{2}\end{align}

\begin{align}\ell_2~:~y=-\frac{4}{1+2t}x+\frac{8}{1+2t}+\frac{1}{2}\end{align}

\begin{align}\ell_2~:~y=-\frac{4}{1+2t}x+\frac{17+2t}{2(1+2t)}\end{align}

\(C\) と \(\ell_2\) の交点 \(\mathrm{Q}\) の \(x\) 座標は\(,\)

\begin{align}-\frac{4}{1+2t}x+\frac{17+2t}{2(1+2t)}=\frac{1}{x}\end{align}

の解のうち\(,\) \(x\neq 2\) の方である. 両辺を \(2x(1+2t)\) 倍して\(,\)

\begin{align}8x^2-(17+2t)x+2(1+2t)=0\end{align}

\begin{align}(x-2)\{8x-(1+2t)\}=0\end{align}

quandle
quandle

一見難しそうな \(2\) 次方程式ですが\(,\) \(C\) と \(\ell_2\) は明らかに \(\mathrm{P}\) を通るので\(,\) \(x=2\) を解にもつ\(,\) つまり\(x-2\) を因数にもつことが分かっています.

\(x\neq 2\) より\(,\)

\begin{align}x=\frac{1+2t}{8}\end{align}

\begin{align}\mathrm{Q}\left(\frac{1+2t}{8},~\frac{8}{1+2t}\right)~~~~\cdots \fbox{答}\end{align}

(4) の解答〜積分で面積を求める〜

\(\displaystyle t=\frac{3}{2}\) のとき\(,\) (1) より\(,\)

\begin{align}\ell_1~:~y=x-\frac{3}{2}\end{align}

(3) より\(,\) \(\mathrm{Q}\left(\frac{1}{2},~2\right)\) より\(,\) \(\ell_3\) の傾きは \(\displaystyle f^{\prime}\left(\frac{1}{2}\right)=-4\) であるから\(,\)

\begin{align}\ell_3~:~y=-4\left(x-\frac{1}{2}\right)+2\end{align}

\begin{align}\ell_3~:~y=-4x+4\end{align}

\(\ell_1\) と \(\ell_3\) の交点を \(\mathrm{R}\) とおくと\(,\) その \(x\) 座標は

\begin{align}x-\frac{3}{2}=-4x+4\end{align}

の解であるから\(,)

\begin{align}5x=\frac{11}{2}\end{align}

\begin{align}x=\frac{11}{10}\end{align}

\begin{align}\mathrm{R}\left(\frac{11}{10},~-\frac{2}{5}\right)\end{align}

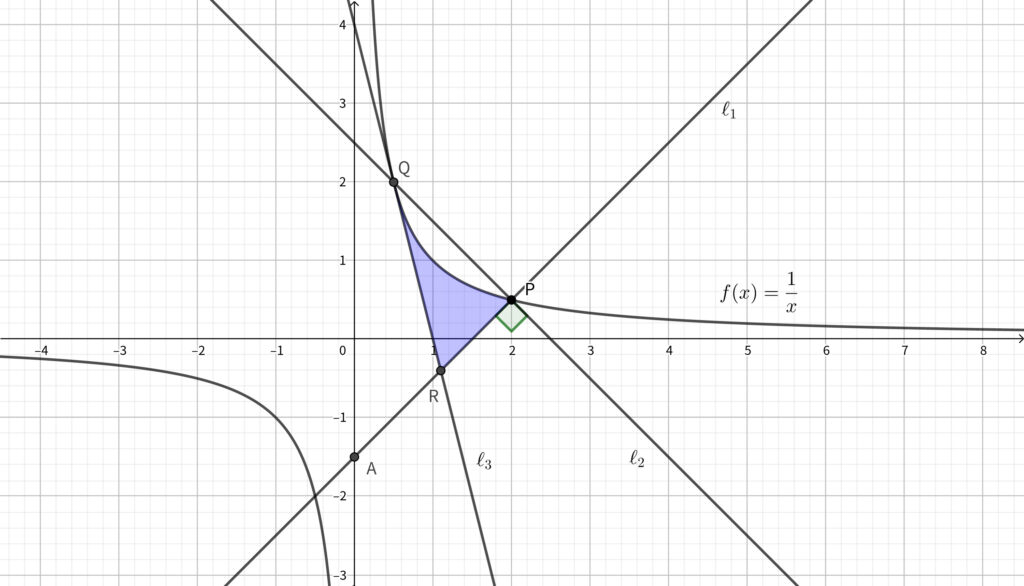
求める面積を \(S\) とおくと\(,\)

\begin{align}S=\int_{\frac{1}{2}}^{\frac{11}{10}}\left\{\frac{1}{x}-(-4x+4)\right\}dx+\int_{\frac{11}{10}}^2\left\{\frac{1}{x}-\left(x-\frac{3}{2}\right)\right\}dx\end{align}

\begin{align}=\biggl[\log{x}+2(x-1)^2\biggr]_{\frac{1}{2}}^{\frac{11}{10}}+\biggl[\log{x}-\frac{1}{2}\left(x-\frac{3}{2}\right)^2\biggr]_{\frac{11}{10}}^2\end{align}

\begin{align}=\log{\frac{11}{10}}+\frac{1}{50}-\log{\frac{1}{2}}-\frac{1}{2}+\log{2}-\frac{1}{8}-\log{\frac{11}{10}}+\frac{2}{25}\end{align}

\begin{align}=\log{4}+\frac{4-100-25+16}{200}=2\log{2}-\frac{21}{40}~~~~\cdots \fbox{答}\end{align}

\(S\) が正の値であることのチェック

\(S\) は面積ですから\(,\) 正の値になるはずです. 検算として \(S>0\) であることをチェックしておきましょう.

\begin{align}S=2\log{2}-\frac{21}{40}\end{align}

でした. 正かどうかが判断できればいいので正確な値を出す必要はありません.

\begin{align}2\log{2}=\log_e{4}>\log_e{e}=1\end{align}

ですから\(,\) \(2\log{2}\) は \(1\) より大きい数であることがわかります. 一方

\begin{align}\frac{21}{40}<\frac{40}{40}=1\end{align}

ですから\(,\) \(\displaystyle \frac{21}{40}\) は \(1\) より小さい数であることがわかります.

よって\(,\)

\begin{align}S=2\log{2}-\frac{21}{40}>0\end{align}

であることがわかりました. 面積や体積を出したら\(,\) 正の値になっているかを確認する癖をつけましょう. それだけで計算ミスをかなり防ぐことができます.

なお\(,\) 関数電卓で計算してみたところ\(,\)

\begin{align}2\log{2}-\frac{21}{40} \fallingdotseq 0.8612943611\end{align}

でした.

スポンサーリンク

コメント

タイトルとURLをコピーしました