東京理科大学工学部2023年第1問(1)

工学部2023年第1問(1)の問題文全文
(a) の解答〜不定形のときは変形を〜
(b) の解答
1. $g(x)$ と $f^{\prime}(x)$ の関係〜$x^2(x^2-1)^2$ は何者か〜
2. $g(x)$ の計算〜$f^{\prime}(x)$ の分子だけを計算〜
(c) の着眼点〜だいたいどの辺でとりそうか見当をつける〜
(c) の解答〜マーク式なので証明はしない〜
1. ＜補足＞「ただ $1$ つ存在する」ことを証明する

工学部2023年第1問(1)の問題文全文

(1) $x>1$ に対して

\begin{align}f(x)=\frac{5x^3+8x^2+15}{x^3-x}\end{align}

とする.

(a) $\displaystyle \lim_{x\to \infty}f(x)=~\fbox{$\hskip0.4emア\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~,~~f(9)=\frac{~\fbox{$\hskip0.4emイウエ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emオカ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~$ である.

(b) $g(x)=x^2(x^2-1)^2f^{\prime}(x)$ とおくと

\begin{align}g^{\prime}(x)=-~\fbox{$\hskip0.4emキク\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~x^3-~\fbox{$\hskip0.4emケコ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~x^2-~\fbox{$\hskip0.4emサシス\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~x\end{align}

である. ただし$,$ $f^{\prime}(x),~g^{\prime}(x)$ はそれぞれ $f(x),~g(x)$ の導関数である.

\begin{align}f(b)=\frac{~\fbox{$\hskip0.4emセソタチ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emツテト\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}

である.

(a) の解答〜不定形のときは変形を〜

\begin{align}\lim_{x\to \infty}f(x)=\lim_{x\to \infty}\cfrac{5+\cfrac{8}{x}+\cfrac{15}{x^3}}{1-\cfrac{1}{x^2}}=5~~~~\cdots \fbox{答}\end{align}

\begin{align}f(9)=\frac{5\cdot 729+8\cdot 81+15}{729-9}=\frac{4308}{720}=\frac{359}{60}~~~~\cdots \fbox{答}\end{align}

ア：５　イ：３　ウ：５　エ：９　オ：６　カ：０

(b) の解答

$g(x)$ と $f^{\prime}(x)$ の関係〜$x^2(x^2-1)^2$ は何者か〜

$f(x)$ の分母を因数分解してみます.

\begin{align}f(x)=\frac{5x^3+8x^2+15}{x(x^2-1)}\end{align}

つまり$,$ 問題文の $x^2(x^2-1)$ は $f(x)$ の分母の $2$ 乗になっていることがわかります.

「分母の $2$ 乗」といえば「商の微分」ですね！

つまり$,$ $g(x)$ は $f^{\prime}(x)$ の分母をはらったもの（＝$f^{\prime}(x)$ の分子）と解釈できます.

$g(x)$ の計算〜$f^{\prime}(x)$ の分子だけを計算〜

\begin{align}g(x)=(15x^2+16x)(x^3-x)-(5x^3+8x^21+15)(3x^2-1)\end{align}

\begin{align}=-8x^4-10x^3-53x^2+15\end{align}

\begin{align}\therefore g^{\prime}(x)=-32x^3-30x^2-106x~~~~\cdots \fbox{答}\end{align}

キ：３　ク：２　ケ：３　コ：０　サ：１　シ：０　ス：６

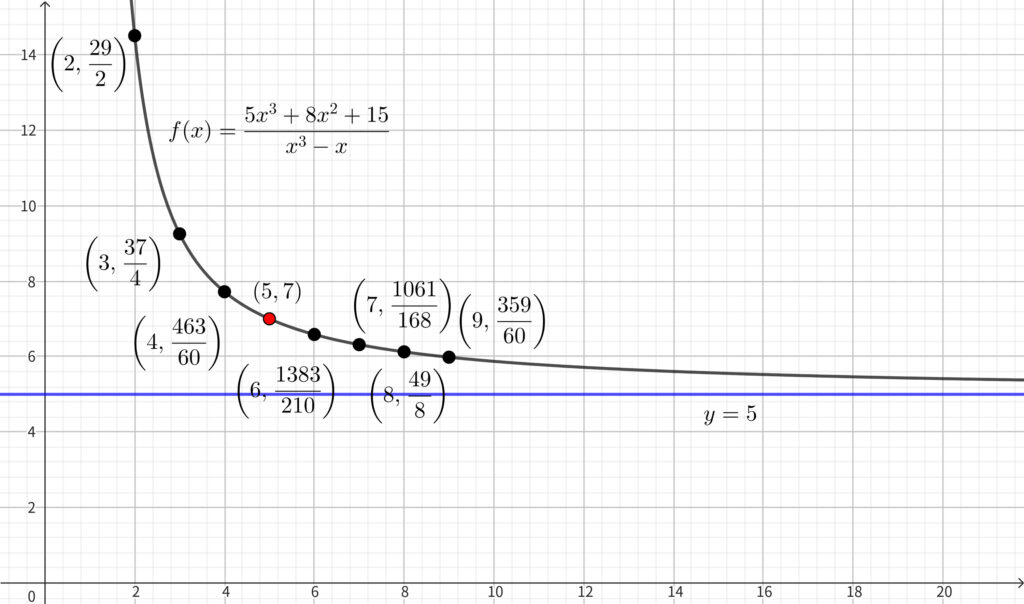
(c) の着眼点〜だいたいどの辺でとりそうか見当をつける〜

注目すべきは

「(a) でわざわざ $f(9)$ を求めている」

ということです. そしてそれは整数値ではないということと$,$ $6$ よりも小さい値であることもポイントです. さらに問題文によると

「$y=f(x)$ を満たす自然数の組 $(x,~y)$ はただ $1$ つ存在する」

という情報（要証明で後述します）があるのと$,$ (a) で

「$\displaystyle \lim_{x\to \infty}f(x)=5$ である」

ということを示したことです.

これらの情報から予想できるのは

「求める自然数の組 $(x,~y)$ は $x$ が $9$ よりも小さいところにありそう」

ということです. $f(x)$ の定義域は $x>1$ ですから$,$ $x$ の候補は

\begin{align}x=2,~3,~4,~5,~6,~7,~8\end{align}

の $7$ 択まで絞られました. あとはどこから調べるかですが$,$ 小さい順にやっていってもいいですし$,$ もう少し候補が絞れるかもしれないので真ん中あたりで調べてみて言えそうなことを考察するということが考えられます. 筆者もどっちで攻めるか迷いましたが$,$ $7$ つ調べるのは大変そうなのでもう少し候補を絞るために真ん中の $x=5$ で一旦調べてみようと考えました.

(c) の解答〜マーク式なので証明はしない〜

\begin{align}f(5)=\frac{625+200+15}{125-5}=\frac{840}{120}=7\end{align}

より$,$ $x,~y$ はともに自然数であるから$,$

\begin{align}(a,~b)=(5,~7)\end{align}

である. このとき$,$

\begin{align}f(7)=\frac{1715+392+15}{343-7}\end{align}

\begin{align}=\frac{2122}{336}=\frac{1061}{168}~~~~\cdots \fbox{答}\end{align}

quandle

とりあえず真ん中あたりでやってみたら「たまたま」一発で見つかりました.
もし$,$ $x=5$ でやってみて整数にならなかったらその周辺をやってみることになると思います.

セ：１　ソ：０　タ：６　チ：１　ツ：１　テ：６　ト：８

＜補足＞「ただ $1$ つ存在する」ことを証明する

今回は穴埋め問題だったのと$,$ 問題文に「ただ $1$ つ存在する」ことを書いてくれているので$,$ 認めてしまえば答えを出すことはすぐにできました. もしこれが記述式の問題だったとしたら$,$ 「ただ $1$ つ存在する」ということを証明する必要があると思います.

「ただ $1$ つ存在する」ことの証明では$,$ 一旦「存在する」ことを証明した上で$,$ ①か②のいずれかを証明すればOKです！

①　具体的に $1$ つ見つけて$,$ それ以外は存在しないこと

②　$a$ と $a^{\prime}$ が存在すると仮定して$,$ $a=a^{\prime}$ であること

今回は $x=5$ という具体的な存在がわかっているので$,$ ①の方針で証明します. そのために示す必要があるのは以下です.

１．$f(x)$ が単調減少関数であること

２．$x\geqq 9$ では $y=f(x)$ は自然数にならないこと

３．$x=2,~3,~4,~6,~7,~8$ のとき $y=f(x)$ は自然数にならないこと

$f(x)$ が単調減少関数であることを証明する〜$f^{\prime}(x)$ の代わりに $g(x)$ を調べる〜

\begin{align}g(x)=x^2(x^2-1)^2f^{\prime}(x)\end{align}

において$,$ (b) より$,$

\begin{align}g^{\prime}(x)=-2x(16x^2+15x+53)\end{align}

であり$,$ $x>1$ において $-2x<0,~16x^2+15x+53>0$ であるから$,$$g^{\prime}(x)<0.$

よって$,$ $x>1$ において $g(x)$ は単調減少であり$,$ $g(1)=0$ より$,$ $g(x)<0.$

ここで$,$ $x^2(x^2-1)^2>0$ であるから$,$ $g(x)$ と $f^{\prime}(x)$ の符号は一致するので$,$

$f^{\prime}(x)<0$ となり$,$ $f(x)$ が $x>1$ において単調減少関数であることが示された.

$x\geqq 9$ では $y=f(x)$ が自然数にならないことの証明

$f(x)$ が $x>1$ において（特に $x\geqq 9$ において）単調減少であることと$,$ (a) より$,$

\begin{align}f(9)=\frac{359}{60}<6,~\lim_{x\to \infty}f(x)=5\end{align}

であることから$,$ $x\geqq 9$ において $y=f(x)$ が自然数になることはない.

$x=2,~3,~4,~6,~7,~8$ のとき $y=f(x)$ は自然数にならないことの証明

\begin{align}f(2)=\frac{40+32+15}{8-2}=\frac{87}{6}=\frac{29}{2}\notin \mathbb{N}\end{align}

\begin{align}f(3)=\frac{135+72+15}{27-3}=\frac{222}{24}=\frac{37}{4}\notin \mathbb{N}\end{align}

\begin{align}f(4)=\frac{320+128+15}{64-4}=\frac{463}{60}\notin \mathbb{N}\end{align}

\begin{align}f(6)=\frac{1080+288+15}{216-6}=\frac{1383}{210}\notin\mathbb{N}\end{align}

\begin{align}f(7)=\frac{1061}{168}\notin \mathbb{N}\end{align}

\begin{align}f(8)=\frac{2560+512+15}{512-8}=\frac{3087}{504}=\frac{49}{8}\notin \mathbb{N}\end{align}

以上より$,$ $x=2,~3,~4,~6,~7,~8$ のとき $y=f(x)$ は自然数にならない.

ここまでの議論をまとめると$,$ $y=f(x)$ を満たす自然数 $(x,~y)$ の組はただ $1$ つ存在して$,$

\begin{align}(x,~y)=(5,~7)\end{align}

である.

東京理科大学工学部2023年第1問(1)

工学部2023年第1問(1)の問題文全文

(a) の解答〜不定形のときは変形を〜

(b) の解答

\(g(x)\) と \(f^{\prime}(x)\) の関係〜\(x^2(x^2-1)^2\) は何者か〜

\(g(x)\) の計算〜\(f^{\prime}(x)\) の分子だけを計算〜

(c) の着眼点〜だいたいどの辺でとりそうか見当をつける〜

(c) の解答〜マーク式なので証明はしない〜

＜補足＞「ただ \(1\) つ存在する」ことを証明する

\(f(x)\) が単調減少関数であることを証明する〜\(f^{\prime}(x)\) の代わりに \(g(x)\) を調べる〜

\(x\geqq 9\) では \(y=f(x)\) が自然数にならないことの証明

\(x=2,~3,~4,~6,~7,~8\) のとき \(y=f(x)\) は自然数にならないことの証明

コメント