工学部2023年第3問の問題文全文
\(a\) と \(b\) を定数 \((a>0,~b<0)\) とする. 実数 \(x\) の関数
\begin{align}f(x)=e^{a+bx},~g(x)=e^{-f(x)}\end{align}
に対して\(,\) 座標平面上の曲線 \(C~:~y=e^{bx}g(x)\) を考える. ただし\(,\) \(e\) は自然対数の底を表す.
(1) \(\displaystyle \lim_{x\to \infty}e^{bx}g(x)=~\fbox{$\hskip0.4em(あ)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) である.
(2) \(\displaystyle \lim_{x\to -\infty}e^{bx}g(x)=~\fbox{$\hskip0.4em(い)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) である. ただし\(,\) \(\displaystyle \lim_{x\to \infty}\frac{x}{e^x}=0\) を用いてよい.
(3) 関数 \(y=e^{bx}g(x)\) は \(x=~\fbox{$\hskip0.4em(う)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) のとき\(,\) 極値 \(y=~\fbox{$\hskip0.4em(え)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) をとる. また\(,\) 曲線 \(C\) の変曲点の \(x\) 座標は \(\fbox{$\hskip0.4em(お)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) および \(\fbox{$\hskip0.4em(か)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) である. ただし\(,\) \(\fbox{$\hskip0.4em(お)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~<~\fbox{$\hskip0.4em(か)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) とする.
(4) \(t\) を正の実数とする. 曲線 \(C\) と \(x\) 軸\(,\) および \(2\) 直線 \(x=-t,~x=t\) で囲まれた部分を\(,\) \(x\) 軸の周りに \(1\) 回転させてできる立体の体積を \(V(t)\) とすると
\begin{align}\lim_{t\to \infty}V(t)=~\fbox{$\hskip0.4em(き)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\end{align}
である.
(1) の解答〜 \(b<0\) であることに注意〜
\begin{align}\lim_{x\to \infty}e^{bx}g(x)=\lim_{x\to \infty}e^{bx}e^{-f(x)}\end{align}
\begin{align}=0\times e^0=0~~~~\cdots \fbox{答}\end{align}
(あ) 0
(2) の解答〜\(\displaystyle \lim_{x\to \infty}\frac{x}{e^x}=0\) が使えるように変形〜
\begin{align}\lim_{x\to -\infty}e^{bx}g(x)=\lim_{x\to -\infty}e^{bx-e^{a+bx}}\end{align}
\begin{align}=\lim_{x\to -\infty}e^{bx\left(1-e^a\cdot \frac{e^{bx}}{bx}\right)}\end{align}
\(t=bx\) とおくと\(,\) \(b<0\) より\(,\) \(x\to -\infty \) のとき\(,\) \(t\to \infty \) であるから\(,\)
\begin{align}=\lim_{t\to \infty}e^{t\left(1-e^a\cdot \frac{e^t}{t}\right)}\end{align}
\(\displaystyle \lim_{t\to \infty}\frac{t}{e^t}=0\) より\(,\) \(\displaystyle \lim_{t\to \infty}\frac{e^t}{t}=\infty\) であるから\(,\)
\begin{align}\lim_{t\to \infty}t\left(1-e^a\cdot \frac{e^t}{t}\right)=-\infty\end{align}
以上より\(,\)
\begin{align}\lim_{t\to \infty}e^{t\left(1-e^a\cdot \frac{e^t}{t}\right)}=0~~~~\cdots \fbox{答}\end{align}
(い)0
(3) の解答〜極値も変曲点も符号の変化を確認〜
\begin{align}y^{\prime}=\left(b-be^{a+bx}\right)e^{bx-e^{a+bx}}=be^{bx-e^{a+bx}}\left(1-e^{a+bx}\right)\end{align}
\(b<0\) より\(,\) \(be^{bx-e^{a+bx}}<0\) であるから\(,\) \(y^{\prime}\) の符号は \(1-e^{a+bx}\) の符号と逆符号になる. \(a+bx=0\) すなわち \(\displaystyle x=-\frac{a}{b}\) の前後で \(y^{\prime}\) の符号は変化する. また\(,\)
\begin{align}y^{\prime \prime}=b\left(b-be^{a+bx}\right)e^{bx-e^{a+bx}}\left(1-e^{a+bx}\right)+be^{bx-e^{a+bx}}\left(-be^{a+bx}\right)\end{align}
\begin{align}=b^2e^{bx-e^{a+bx}}\left\{\left(e^{a+bx}\right)^2-3e^{a+bx}+1\right\}\end{align}
\(b^2e^{bx-e^{a+bx}}>0\) より\(,\) \(y^{\prime \prime}\) の符号と \(\left(e^{a+bx}\right)^2-3e^{a+bx}+1\) の符号は一致する.
ここで\(,\) \(X=e^{a+bx}(>0)\) とおくと\(,\) \(X^2-3X+1=0\) のとき\(,\) \(y^{\prime \prime}=0\) となる.
\(X^2-3X+1=0\) を解くと\(,\)
\begin{align}X=\frac{3\pm \sqrt{5}}{2}\end{align}
が得られるが\(,\) どちらも \(X>0\) を満たしている. このとき\(,\)
\begin{align}e^{a+bx}=\frac{3\pm \sqrt{5}}{2}\end{align}
\begin{align}a+bx=\log{\frac{3\pm \sqrt{5}}{2}}\end{align}
\begin{align}\therefore x=\frac{1}{b}\left(\log{\frac{3\pm \sqrt{5}}{2}}-a\right)\end{align}
\(b<0\) であることと\(,\) 関数 \(y=\log{x}\) が単調増加であることから\(,\)
\begin{align}\frac{1}{b}\left(\log{\frac{3+\sqrt{5}}{2}}-a\right)<\frac{1}{b}(\log{1}-a)<\frac{1}{b}\left(\log{\frac{3-\sqrt{5}}{2}}-a\right)\end{align}
よって\(,\) 増減と凹凸は以下の表のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|}\hline x & \cdots & \displaystyle \frac{1}{b}\left(\log{\frac{3+\sqrt{5}}{2}}-a\right) & \cdots & \displaystyle -\frac{a}{b} & \cdots & \displaystyle \frac{1}{b}\left(\log{\frac{3-\sqrt{5}}{2}}-a\right) & \cdots \\ \hline y^{\prime} & + & + & + & 0 & – & – & – \\ \hline y^{\prime \prime} & + & 0 & – & – & – & 0 & + \\ \hline y & \nearrow \cup & {} & \nearrow \cap & e^{-a-1} & \searrow \cap & {} & \searrow \cup \\ \hline \end{array}\end{align}
増減表より\(,\)
\begin{align}x=-\frac{a}{b}~のとき~極大値~e^{-a-1}~をとる ~~~~\cdots \fbox{答}\end{align}
\begin{align}変曲点の~x~座標は~x=\frac{1}{b}\left(\log{\frac{3+\sqrt{5}}{2}}-a\right),~\frac{1}{b}\left(\log{\frac{3-\sqrt{5}}{2}}-a\right)~~~~\cdots \fbox{答}\end{align}
\begin{align}(う)~ -\frac{a}{b}~(え)~e^{-a-1}~(お)~\frac{1}{b}\left(\log{\frac{3+\sqrt{5}}{2}}-a\right)~(か)~\frac{1}{b}\left(\log{\frac{3-\sqrt{5}}{2}}-a\right)\end{align}
(4) の解答〜置換積分を利用して計算量を減らす〜
グラフの概形をつかむ〜これまでやってきたことを整理する〜
(3) より\(,\) \(y=e^{bx}g(x)\) の増減および凹凸がわかっていて\(,\) (1) と (2) により\(,\) \(x\to \infty \) および \(x\to -\infty \) がわかっているので\(,\) グラフの概形は以下のようになる.
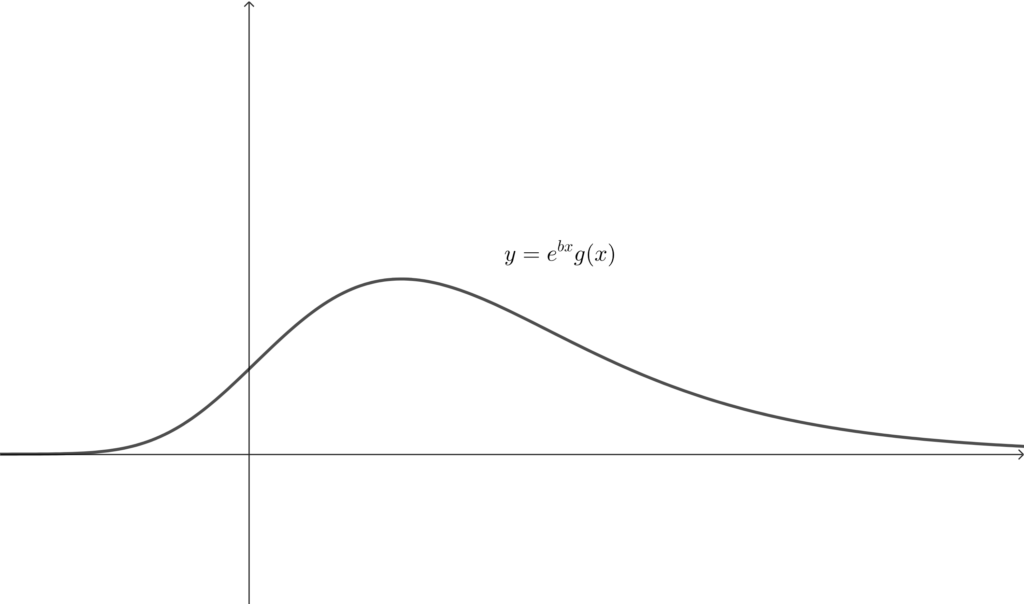

quandle
\(y=e^{bx}g(x)\) のグラフは \(x\) 軸よりも上にあることがわかりますね. 体積の計算式は非常にシンプルになります.
\(V(t)\) を立式する〜回転体の体積公式をそのまま適用〜
\begin{align}V(t)=\pi \int_{-t}^t\left(e^{bx-e^{a+bx}}\right)^2dx\end{align}

quandle
いきなり手が止まってしまう積分が出てきました. 筆者は初手がなかなか思いつかず苦戦しました. 文字が多く見通しが立たないので \(u=e^{bx}\) とおいて少しでも見た目が簡単にならないかなとやってみました. 積分範囲が逆に汚くなってしまうのでなかなか勇気のいる置換でした.
\(u=e^{bx}\) とおくと\(,\) \(du=budx\) より\(,\) \(\displaystyle dx=\frac{1}{bu}du\) であり\(,\)
\begin{align}\begin{array}{|c|ccc|} \hline x & -t & \to & t \\ \hline u & e^{-bt} & \to & e^{bt}\\ \hline \end{array}\end{align}
であるから\(,\)
\begin{align}=\pi \int_{e^{-bt}}^{e^{bt}}\left(u\cdot e^{-e^au}\right)^2\cdot \frac{1}{bu}du=\frac{\pi}{b}\int_{e^{-bt}}^{e^{bt}}u\cdot e^{-2e^au}du\end{align}
\(s=e^{-bt}\) とおくと\(,\)
\begin{align}V(t)=\frac{\pi}{b}\int_s^{\frac{1}{s}}u\cdot e^{-2e^au}du\end{align}
\(\displaystyle \int_s^{\frac{1}{s}}u\cdot e^{-2e^au}du\) を求める〜部分積分の利用〜
\begin{align}W(s)=\int_s^{\frac{1}{s}}u\cdot e^{-2e^au}du\end{align}
\begin{align}=\biggl[-\frac{u}{2e^a}e^{-2e^au}\biggr]_s^{\frac{1}{s}}-\int_s^{\frac{1}{s}}-\frac{1}{2e^a}e^{-2e^au}du\end{align}
\begin{align}=-\frac{1}{2e^a}\cdot \frac{e^{-2e^a\cdot \frac{1}{s}}}{s}+\frac{e^{2e^a}}{2e^a}\cdot \frac{s}{e^s}-\frac{1}{4e^{2a}}\left(e^{-2e^a\cdot \frac{1}{s}}-e^{-2e^as}\right)\end{align}
\(\displaystyle \lim_{t\to \infty}V(t)\) を求める〜不定形はなさそう〜
\(t\to \infty \) のとき\(,\) \(b<0\) より\(,\) \(s\to \infty \)であるから\(,\)
\begin{align}\lim_{t\to \infty}V(t)=\lim_{s\to \infty}\frac{\pi}{b}W(s)\end{align}
\begin{align}=\frac{\pi}{b}\left\{-\frac{1}{2e^a}\cdot 0+\frac{e^{2e^a}}{2e^a}\cdot 0 -\frac{1}{4e^{2a}}(1-0)\right\}\end{align}
\begin{align}=\frac{\pi}{b}\cdot \left(-\frac{1}{4e^{2a}}\right)=-\frac{\pi}{4e^{2a}b}~~~~\cdots \fbox{答}\end{align}

quandle
不定形なのは \(\displaystyle \lim_{s\to \infty}\frac{s}{e^s}\) だけです. これも(2) の問題文で \(0\) であることを教えてくれているので即極限値が求められますね!
(き) \(\displaystyle -\frac{\pi}{4e^{2a}b}\)








コメント