公立山口工学部推薦2023年(18)(19)の問題文全文
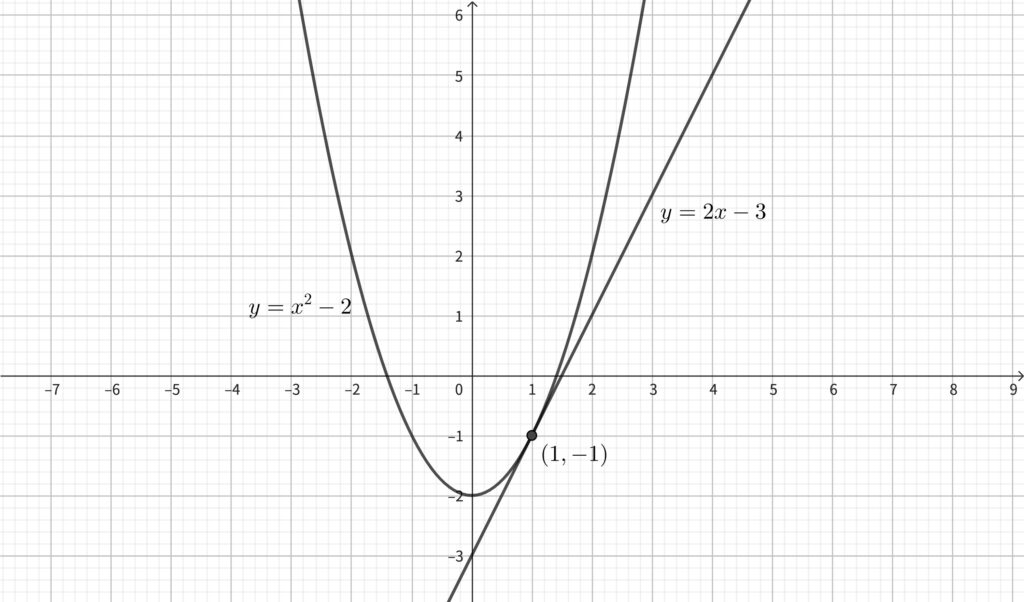
(18) 関数 \(y=x^2-2\) のグラフ上の点 \(\mathrm{A}(1,~-1)\) における接線の方程式を求めなさい.
(19) 放物線 \(y=x^2+2\) と \(x\) 軸\(,\) および \(2\) つの直線 \(x=0,~x=2\) で囲まれた部分の面積を求めなさい.
(18) の解答〜接線の公式を利用〜
\begin{align}y^{\prime}=2x\end{align}
より\(,\) \(x=1\) のとき\(,\) \(y^{\prime}=2\) であるから\(,\) 求める接線の方程式は\(,\)
\begin{align}y=2(x-1)-1\end{align}
\begin{align}\therefore y=2x-3~~~~\cdots \fbox{答}\end{align}
(19) の解答〜面積は積分で求める〜
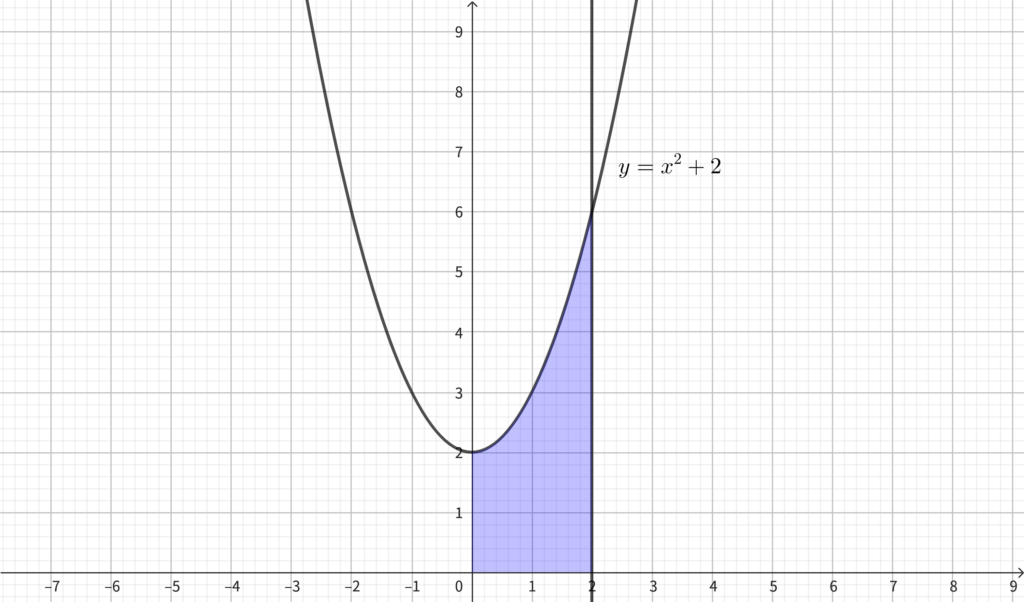
上図より\(,\) 求める面積は\(,\)
\begin{align}\int_0^2(x^2+2)dx=\biggl[\frac{1}{3}x^3+2x\biggr]_0^2\end{align}
\begin{align}=\frac{8}{3}+4=\frac{20}{3}~~~~\cdots \fbox{答}\end{align}




コメント