問題文全文
座標平面において\(,\) 曲線 \(y=x^2\) と中心 \(\displaystyle \left(0,~\frac{3}{4}\right)\) の円が 2 つの異なる共有点で接しているとし\(,\) それらの共有点を \(\mathrm{A},~\mathrm{B}\) とする. ただし\(,\) 曲線と円が接するとは\(,\) 曲線と円が共有点で共通の接線をもつことである. この円の方程式は\(,\)
\begin{align}x^2+\left(y-\frac{3}{4}\right)^2=\frac{\fbox{$\hskip0.8emネ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emノ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である. 弧 \(\mathrm{AB}\) と曲線 \(y=x^2\) で囲まれる図形を \(C_1\) とする. \(C_1\) の面積は\(,\)
\begin{align}\frac{\fbox{$\hskip0.8emハ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emヒフ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\frac{\fbox{$\hskip0.8emヘ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emホ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\end{align}
である. ただし\(,\) 円周上の 2 点 \(\mathrm{P},~\mathrm{Q}\) に対し\(,\) 弧 \(\mathrm{PQ}\) とは短い方の弧をさす.
曲線 \(y=4x^2\) と中心 \((0,~a),\) 半径 \(r\) の円が 2 つの異なる共有点で接しているとし\(,\) その共有点を \(\mathrm{C},~\mathrm{D}\) とする. 弧 \(\mathrm{CD}\) と曲線 \(y=4x^2\) で囲まれる図形を \(C_2\) とする. \(C_1\) と \(C_2\) が相似であるとき\(,\)
\begin{align}a=\frac{\fbox{$\hskip0.8emマ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emミム\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}},~~r=\frac{\sqrt{\fbox{$\hskip0.8emメ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emモ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
であり\(,~C_2\) の面積は\(,\)
\begin{align}\frac{\fbox{$\hskip0.8emヤ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emユヨラ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\frac{\fbox{$\hskip0.8emリ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emルレロ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\end{align}
である.
前半:C_1 の面積までの解答
\begin{align}x^2+\left(y-\frac{3}{4}\right)^2=R^2\end{align}
とおく. \(y=x^2\) と連立して\(,\)
\begin{align}y+\left(y-\frac{3}{4}\right)^2=R^2\end{align}
\begin{align}y^2-\frac{1}{2}y-R^2+\frac{9}{16}=0~~~~\cdots ①\end{align}

quandle
放物線も円も \(y\) 軸対称なので\(,\) 2 つの接点の \(y\) 座標は同じになりますね. ①が重解をもてばいいことになります.
これの判別式を \(D_1\) とおくと\(,~D_1=0\) より\(,\)
\begin{align}D_1=\left(-\frac{1}{2}\right)^2-4\cdot 1\cdot \left(-R^2+\frac{9}{16}\right)=0\end{align}
\begin{align}4R^2-2=0\end{align}
\begin{align}R^2=\frac{1}{2}\end{align}
よって\(,\) 求める円の方程式は
\begin{align}x^2+\left(y-\frac{3}{4}\right)^2=\frac{1}{2}\end{align}
① より\(,\)
\begin{align}y^2-\frac{1}{2}y+\frac{1}{16}=0\end{align}
\begin{align}\left(y-\frac{1}{4}\right)^2=0\end{align}
よって\(,\)
\begin{align}y=\frac{1}{4}\end{align}
\(\displaystyle x^2=\frac{1}{4}\) より\(\displaystyle ,~x=\pm \frac{1}{2}\) であるから\(,\)
\begin{align}\mathrm{A}\left(-\frac{1}{2},~\frac{1}{4}\right),~\mathrm{B} \left(-\frac{1}{2},~\frac{1}{4}\right)\end{align}
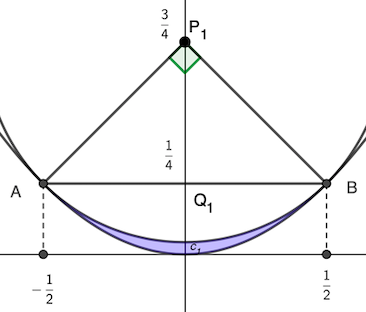
\(\displaystyle \left(0.~\frac{3}{4}\right)\) を点 \(\displaystyle \mathrm{P_1},~\left(0,~\frac{1}{4}\right)\) を点 \(\mathrm{Q_1}\) とおくと\(,\)
\begin{align}\mathrm{P_1A}=\mathrm{P_1B}=R=\frac{1}{\sqrt{2}},~\mathrm{AB}=\frac{1}{2}-\left(-\frac{1}{2}\right)=1\end{align}
であることから\(\displaystyle ,~\angle \mathrm{AP_1B}=\frac{\pi}{2}\) である.
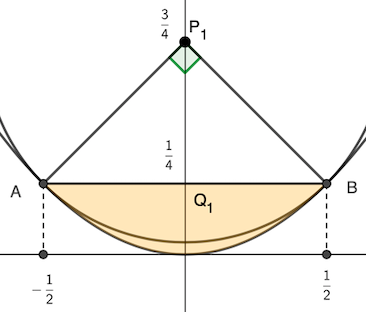
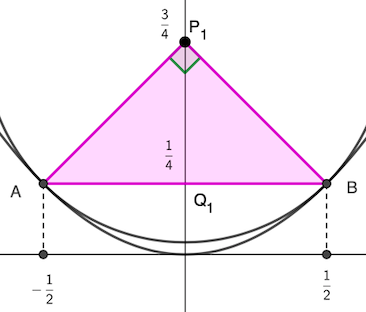
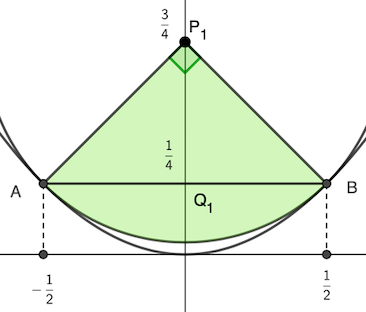
よって\(,\) 求める面積(下図のブルー)は(ブルー)=(オレンジ)+(ピンク)ー(グリーン)によって求められる.

quandle
(オレンジ)の面積は \(\displaystyle \frac{1}{6}\) 公式\(,\) (ピンク)は直角二等辺三角形の面積\(,\) (グリーン)は半径 \(R,\) 中心角 \(\displaystyle \frac{\pi}{2}\) の扇型の面積としてそれぞれ求められますね.
よって\(,~C_1\) の面積は\(,\)
\begin{align}\int_{-\frac{1}{2}}^{\frac{1}{2}}\left(\frac{1}{4}-x^2\right)dx+\frac{1}{2}\cdot R^2-\frac{1}{2}\cdot R^2\cdot \frac{\pi}{2}\end{align}
\begin{align}=-\int_{-\frac{1}{2}}^{\frac{1}{2}}\left(x-\frac{1}{2}\right)\left(x+\frac{1}{2}\right)dx-\frac{1}{8}\pi+\frac{1}{4}\end{align}
\begin{align}=\frac{1}{6}\left\{\frac{1}{2}-\left(-\frac{1}{2}\right)\right\}^3-\frac{1}{8}\pi+\frac{1}{4}=\frac{5}{12}-\frac{1}{8}\pi.\end{align}
後半の解答
\(x^2+(y-a)^2=r^2\) と \(y=4x^2\) を連立して\(,\)
\begin{align}\frac{y}{4}+(y-a)^2=r^2\end{align}
\begin{align} y^2+\left(\frac{1}{4}-2a\right)y+a^2-r^2=0~~~~\cdots ②\end{align}
これの判別式を \(D_2\) とおくと\(,~D_2=0\) より\(,\)
\begin{align}D_2=\left(\frac{1}{4}-2a\right)^2-4\cdot 1\cdot (a^2-r^2)=0\end{align}
\begin{align} 4r^2-a+\frac{1}{16}=0\end{align}
よって\(,\)
\begin{align}r^2=\frac{16-1}{64}\end{align}
② より\(,\)
\begin{align}y^2+\left(\frac{1}{4}-2a\right)y+a^2-\frac{16a-1}{64}=0\end{align}
\begin{align} y^2+\left(\frac{1}{4}-2a\right)y+\frac{64a^2-16a+1}{64}=0\end{align}
\begin{align} \left(y-\frac{8a-1}{8}\right)^2=0\end{align}
よって\(,\)
\begin{align}y=\frac{8a-1}{8}\Leftrightarrow 4x^2=\frac{8a-1}{8}\end{align}
より\(,\)
\begin{align}x=\pm\sqrt{\frac{8a-1}{32}}=\pm\frac{\sqrt{2(8a-1)}}{16}\end{align}
\begin{align}\mathrm{C}\left(-\frac{\sqrt{2(8a-1)}}{16},~\frac{8a-1}{8}\right),~\mathrm{D}\left(\frac{\sqrt{2(8a-1)}}{16},~\frac{8a-1}{8}\right)\end{align}

quandle
\(\mathrm{C,~D}\) の座標を求めるまでの流れは\(\mathrm{A,~B}\) の座標を求めるまでの流れと全く同じです.
ここで\(,\) 点 \(\mathrm{P_2}(0,~a)\) とおくと\(,\)
\begin{align}\overrightarrow{\mathrm{P_2C}}=\left(\frac{\sqrt{2(8a-1)}}{16},~\frac{1}{8}\right),~\overrightarrow{\mathrm{P_2D}}=\left(-\frac{\sqrt{2(8a-1)}}{16},~\frac{1}{8}\right)\end{align}
2020-1024x779.jpg)
\(C_1\) と \(C_2\) が相似であることより\(,~\angle \mathrm{CP_2D}=90^{\circ}\) であるから\(,\)
\begin{align}\overrightarrow{\mathrm{P_2C}}\cdot \overrightarrow{\mathrm{P_2D}}=0\end{align}
\begin{align} -\left\{\frac{\sqrt{2(8a-1)}}{16}\right\}^2+\left(\frac{1}{8}\right)^2=0\end{align}
\begin{align} \frac{-16a+3}{64}=0\end{align}
よって\(,\)
\begin{align}a=\frac{3}{16}.\end{align}

quandle
今回はベクトルの内積を使いましたが\(,\) 2 直線の傾きの積が -1 になることを使っても同じ結果が得られます.
このとき\(,\)
\begin{align}r^2=\dfrac{16\cdot \dfrac{3}{16}-1}{64}=\frac{1}{32}\end{align}
\(r>0\) より\(,\)
\begin{align}r=\frac{1}{4\sqrt{2}}=\frac{\sqrt{2}}{8}.\end{align}
\(C_1\) と \(C_2\) は相似であることより\(,~C_1\) と \(C_2\) の面積比は\(,\)
\begin{align}R^2~:~r^2=\frac{1}{2}~:~\frac{1}{32}=16~:~1\end{align}
であるから\(,~C_2\) の面積は\(,\)
\begin{align}\frac{1}{16}\left(\frac{5}{12}-\frac{1}{8}\pi\right)=\frac{5}{195}-\frac{1}{128}\pi.\end{align}



2020-1024x779.jpg)





コメント