問題文全文
\(xy\) 平面において\(,\) \(x\) 軸\(,\) 直線 \(y=x+2,\) さらに放物線 \(y=x^2\) の右半分 (\(x\geqq 0\) の範囲にある放物線の部分)の \(3\) つで囲まれた図形を\(,\) \(x\) 軸の周りに \(1\) 回転してできる立体の体積は
\begin{align}\frac{\fbox{$\hskip0.8emアイウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emエオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~\pi\end{align}
であり\(,\) \(y\) 軸の周りに \(1\) 回転してできる立体の体積は
\begin{align}\frac{\fbox{$\hskip0.8emカキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~\pi\end{align}
である.
\(x\) 軸回転の解答
求める体積を \(V_x\) とおく.
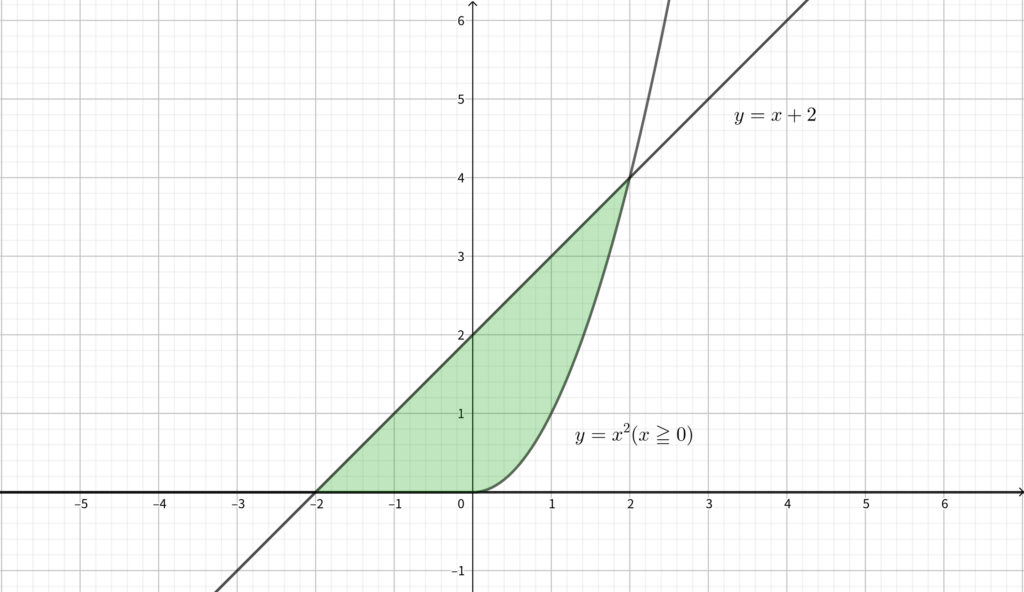
\begin{align}V_x=\frac{1}{3}\cdot 4^2\pi -\pi\int_0^2(x^2)^2dx\end{align}
\begin{align}\frac{V_x}{\pi}=\frac{64}{3}-\biggl[\frac{1}{5}x^5\biggr]_0^2=\frac{64}{3}-\frac{32}{5}\end{align}
\begin{align}=\frac{320-96}{15}=\frac{224}{15}\end{align}
\begin{align}V_x=\frac{224}{15}\pi ~~~~\cdots\fbox{答}\end{align}
ア:2 イ:2 ウ:4 エ:1 オ:5
\(y\) 軸回転の解答
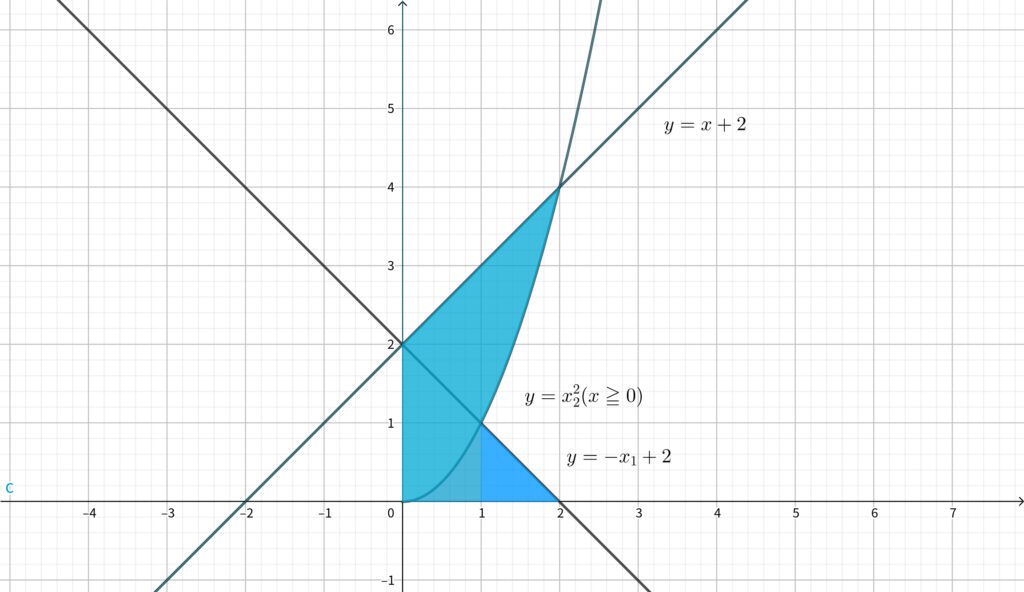
\(y\) 軸に関して折り返した上図を \(y\) 軸に関して \(1\) 回転させてできる立体の体積 \(V_y\) を求める.
\(x\) を区別するため \(y=-x_1+2,~y=x_2^2\) としておく.
\begin{align}V_y=\pi\int_0^1x_1^2dy+\pi\int_1^4x_2^2dy-\frac{1}{3}\cdot 2^2\pi \cdot 2\end{align}
\begin{align}\frac{V_y}{\pi}=\int_0^1(2-y)^2dy+\int_1^4ydy-\frac{8}{3}\end{align}
\begin{align}=\biggl[-\frac{1}{3}(2-y)^3\biggr]_0^1+\biggl[\frac{1}{2}y^2\biggr]_1^4-\frac{8}{3}\end{align}
\begin{align}=-\frac{1}{3}(1-8)+\frac{1}{2}(16-1)-\frac{8}{3}=\frac{14+45-16}{6}=\frac{43}{6}\end{align}
\begin{align}V_y=\frac{43}{6}\pi ~~~~\cdots \fbox{答}\end{align}

quandle
\begin{align}\int (2-y)^2=-\frac{1}{3}(2-y)^3+C\end{align}
は計算ミスしやすいので注意しましょう.
\begin{align}\int f(ax+b)dx=\frac{1}{a}F(ax+b)+C\end{align}
なので\(,\) マイナスがつきます.
カ:4 キ:3 ク:6

2009年第1問1-1.jpg)
2009年第1問1-120x68.jpg)

コメント