公立諏訪東京理科大学工学部中期2021年第４問| 理科大の微積分

公立諏訪　中期　2021年第４問

公立諏訪【中期】

2021.10.23

問題文全文
(1) の解答
(2) の解答
(3) の解答
(4) の着眼点
(4) の解答
(5) の解答

問題文全文

$f(x)=e^{-x}\sin{x}$ として $,$ 曲線 $K~:~y=f(x)$ と $x$ 軸の $x\geqq 0$ の部分との共有点の $x$ 座標を小さい方から順に $p_0,~p_1,~p_2,~\cdots ,~p_n, \cdots$ とおき $,$ 曲線 $K$ と $x$ 軸の $p_{n-1}\leqq x\leqq p_n$ の部分で囲まれる図形の面積を $S_n~(n\geqq 1)$ とおくとき $,$ 以下の問いに答えなさい.

(1) $p_n$ を求めなさい.

(2) $0\leqq x\leqq 2 \pi$ の範囲で関数 $f(x)$ の極値と曲線 $K$ の変曲点を求めなさい.

(3) $S_1$ を求めなさい.

(4) $S_n$ を $S_1$ を用いて表しなさい.

(5) $\displaystyle \sum_{n=1}^{\infty}S_n$ を求めなさい.

(1) の解答

$\begin{align}e^{-x}\sin{x}=0\end{align}$

$e^{-x}>0$ より $,$

$\begin{align}\sin{x}=0\end{align}$

$\begin{align}x=n\pi~(n\geqq 0)\end{align}$

$\begin{align}p_n=n\pi~(n\geqq 0)~~~~\cdots \fbox{答}\end{align}$

(2) の解答

$\begin{align}f^{\prime}(x)=-e^{-x}\sin{x}+e^{-x}\cos{x}\end{align}$

$\begin{align}=e^{-x}\sin{\left(x+\frac{3}{4}\pi \right)}\end{align}$

$0\leqq x\leqq 2\pi$ より $,$

$\begin{align}\frac{3}{4}\pi \leqq x+\frac{3}{4}\pi \leqq \frac{11}{4}\pi \end{align}$

であるから $,$ $f^{\prime}(x)=0$ のとき $,$

$\begin{align}x+\frac{3}{4}\pi =\pi ,~2\pi \end{align}$

$\begin{align}x=\frac{\pi}{4},~\frac{5}{4}\pi \end{align}$

$\begin{align}f^{\prime \prime}(x)=-e^{-x}\sin{\left(x+\frac{3}{4}\pi \right)}+e^{-x}\cos{\left( x+\frac{3}{4}\pi \right)}\end{align}$

$\begin{align}=e^{-x}\sin{\left(x+\frac{3}{2}\pi \right)}\end{align}$

$0\leqq x\leqq 2\pi$ より $,$

$\begin{align}\frac{3}{2}\pi \leqq x+\frac{3}{2}\pi \leqq \frac{7}{2}\pi \end{align}$

なので $,$ $f^{\prime \prime}(x)=0$ のとき $,$

$\begin{align}x+\frac{3}{2}\pi =2\pi ,~3\pi \end{align}$

$\begin{align}x=\frac{\pi}{2},~\frac{3}{2}\pi \end{align}$

よって $,$ 増減表は以下のようになる.

$\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline x & 0 & \cdots & \displaystyle \frac{\pi}{4} & \cdots & \displaystyle \frac{\pi}{2} & \cdots & \displaystyle \frac{5}{4}\pi & \cdots & \displaystyle \frac{3}{2}\pi & \cdots & 2\pi \\ \hline f^{\prime}(x) & {} & + & 0 & – & – & – & 0 & + & + & + & {} \\ \hline f^{\prime \prime}(x) & {} & – & – & – & 0 & + & + & + & 0 & – & {} \\ \hline f(x) & 0 & \nearrow \cap & \displaystyle \frac{1}{\sqrt{2}e^{\frac{\pi}{4}}} & \searrow \cap & e^{-\frac{\pi}{2}} & \searrow \cup & \displaystyle \frac{1}{\sqrt{2}e^{\frac{5}{4}\pi}} & \nearrow \cup & -e^{-\frac{3}{2}\pi} & \nearrow \cap & 0 \\ \hline \end{array}\end{align}$

増減表より $,$

$\begin{align}x=\frac{\pi}{4}~のとき~~極大値 ~\frac{1}{\sqrt{2}e^{\frac{\pi}{4}}}~~~~\cdots \fbox{答}\end{align}$

$\begin{align}x=\frac{5}{4}\pi ~のとき~~極小値~-\frac{1}{\sqrt{2}e^{\frac{5}{4}\pi}}~~~~\cdots \fbox{答}\end{align}$

$\begin{align}変曲点~~\left(\frac{\pi}{2},~e^{-\frac{\pi}{2}}\right),~\left(\frac{3}{2}\pi ,~-e^{-\frac{3}{2}\pi}\right) ~~~~\cdots \fbox{答}\end{align}$

(3) の解答

(1) で求めた $x$ 切片と (2) の増減表から $,$ $y=f(x)$ のグラフは下図のようになる.

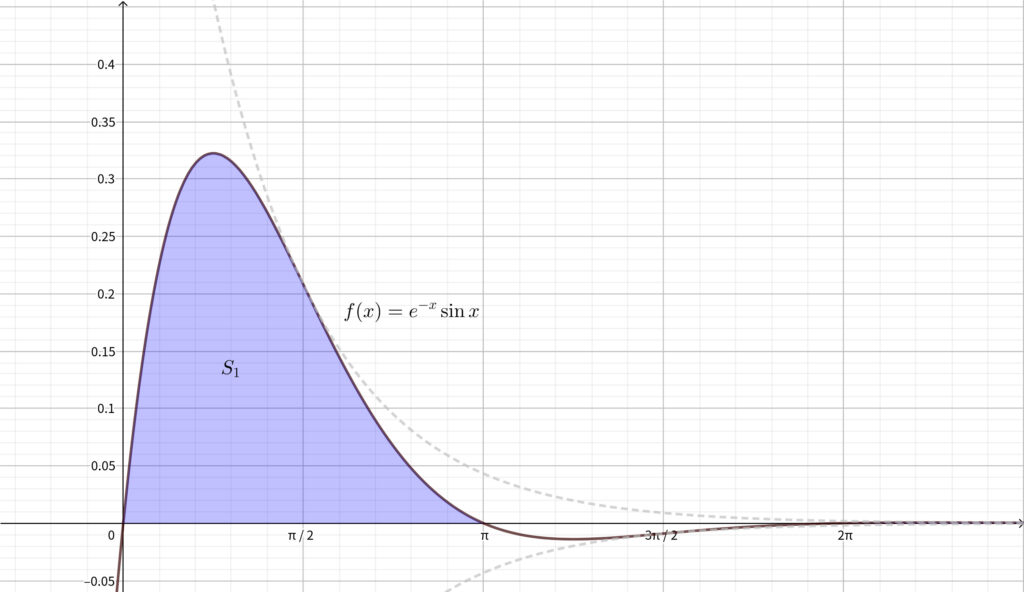
$\begin{align}S_1=\int_0^{\pi}e^{-x}\sin{x}dx\end{align}$

$\begin{align}=\biggl[e^{-x}(-\cos{x})\biggr]_0^{\pi}-\int_0^{\pi}-e^{-x}(-\cos{x})dx\end{align}$

$\begin{align}=e^{-\pi}+1-\int_0^{\pi}e^{-x}\cos{x}dx\end{align}$

$\begin{align}=e^{-\pi}+1-\left(\biggl[e^{-x}\sin{x}\biggr]_0^{\pi}-\int_0^{\pi}-e^{-x}\sin{x}dx\right)\end{align}$

$\begin{align}=e^{-\pi}+1-S_1\end{align}$

$\begin{align}2S_1=e^{-\pi}+1\end{align}$

$\begin{align}S_1=\frac{e^{-\pi}+1}{2}~~~~\cdots \fbox{答}\end{align}$

(4) の着眼点

「 $S_n$ を $S_1$ で表せ.」

と言われています.

$S_n$ の定義域は $(n-1)\pi \leqq x\leqq n\pi$ です. これを $S_1$ で表すということは $,$ その定義域が $0\leqq x\leqq \pi$ となってくれればいいのではないかと考えます.

経験がないとなかなか思いつかないかもしれませんが $,$

$\begin{align}t=x-(n-1)\pi\end{align}$

とおくことでうまく定義域を変更できます.

(4) の解答

$\begin{align}S_n=\left|\int_{(n-1)\pi}^{n\pi}e^{-x}\sin{x}dx\right|\end{align}$

$t=x-(n-1)\pi$ とおくと $,$ $dt=dx$ であり $,$

$\begin{align}\begin{array}{c|ccc}x & (n-1)\pi & \to & n\pi \\ \hline t & 0 & \to & \pi\end{array}\end{align}$

であるから $,$

$\begin{align}S_n=\left|\int_0^{\pi}e^{-\{t+(n-1)\pi\}}\sin{\{t+(n-1)\pi\}}dt\right|\end{align}$

$\begin{align}=\left|e^{-(n-1)\pi}\int_0^{\pi}e^{-t}\cdot (-1)^{n-1}\sin{t}dt\right|\end{align}$

$\begin{align}=\left|e^{-(n-1)\pi}\right|\left|(-1)^{n-1}\right|\left|\int_0^{\pi}e^{-t}\sin{t}dt\right|\end{align}$

$e^{-(n-1)\pi}>0$ $,$ $|(-1)^{n-1}|=1$ $,$ $S_1>0$ より $,$

$\begin{align}S_n=e^{-(n-1)\pi}S_1~~~~\cdots \fbox{答}\end{align}$

(5) の解答

初項 $S_1$ $,$ 公比 $e^{-\pi}$ の無限等比級数の和であるから $,$

$\begin{align}\sum_{n=1}^{\infty}S_n=\frac{1}{1-e^{-\pi}}S_1\end{align}$

$\begin{align}=\frac{e^{\pi}}{e^{\pi}-1}\cdot \frac{e^{-\pi}+1}{2}=\frac{1+e^{\pi}}{2(e^{\pi}-1)}~~~~\cdots \fbox{答}\end{align}$

quandle

初項 $a$ $,$ 公比 $r~(|r|<1)$ の無限等比級数の和は

$\begin{align}\frac{a}{1-r}\end{align}$

でしたね.