創域理工学部(建築・先化・電電・航空宇宙・社基工)2023年第3問の問題文全文
\(k>0,~m>0\) とし\(,\) \(x\geqq 0\) に対して
とおく. ただし\(,\) \(e\) は自然対数の底とする. さらに\(,\) 座標平面上の曲線 \(y=f(x)~(x\geqq 0)\) を \(C_1\)\(,\) 曲線 \(y=g(x)~(x\geqq 0)\) を \(C_2\) とおく. 以下\(,\) \(a>0\) とする.
(1) 点 \((a,~f(a))\) における曲線 \(C_1\) の接線の方程式を\(,\) \(a\) と \(k\) を用いて表せ.
(2) 点 \((a,~g(a))\) における曲線 \(C_2\) の接線の方程式を\(,\) \(a\) と \(m\) を用いて表せ.
以下\(,\) 曲線 \(C_1,~C_2\) がある点 \(\mathrm{P}\) を共有し\(,\) \(\mathrm{P}\) における \(C_1\) と \(C_2\) の接線が一致するとする.
(3) 点 \(\mathrm{P}\) の \(x\) 座標を \(b\) とするとき\(,\) \(b\) と \(m\) を\(,\) \(k\) を用いて表せ.
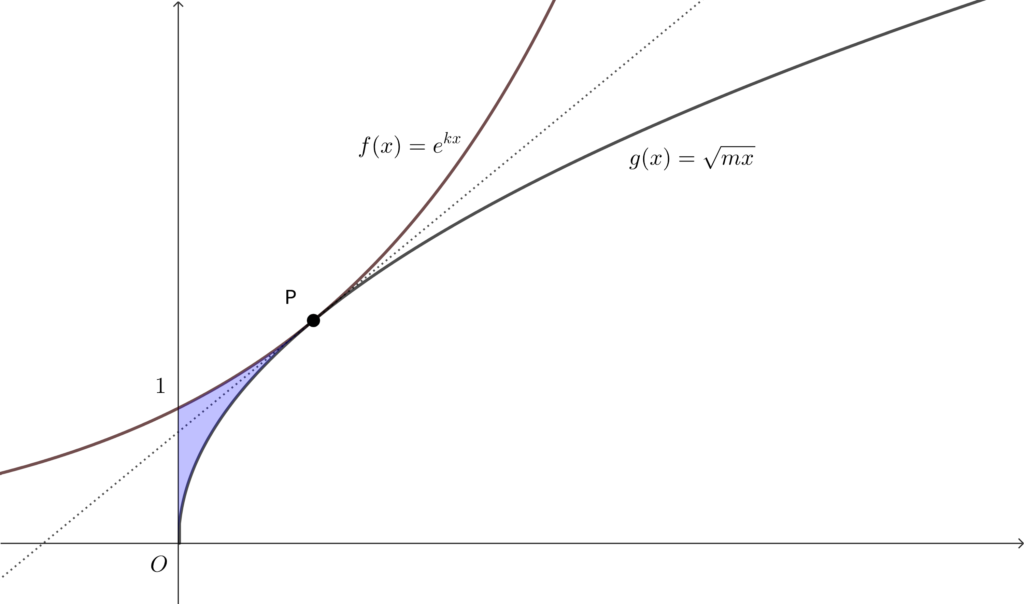
(4) 曲線 \(C_1,~C_2\) および \(y\) 軸で囲まれた図形の面積を\(,\) \(k\) を用いて表せ.
(1) の解答〜公式に当てはめるだけ〜
より\(,\) \((a,e^{ka})\) における接線の方程式は
(2) の解答〜微分可能な \(x\) の範囲に注意〜
\(x>0\) において\(,\)
より\(,\) \((a,~\sqrt{ma})\) における接線の方程式は

\(y=g(x)\) の定義域は \(x\geqq 0\) ですが\(,\) 微分可能な \(x\) の範囲は \(x>0\) なので最初に「\(x>0\) において」と断りましょう. \(a>0\) という条件がありますから\(,\) \(x=a\) を \(y=g^{\prime}(x)\) に代入する行為は問題なく\(,\) \(g^{\prime}(a)\) という値が自然に定義されます.
(3) の解答〜(1) と (2) を連立〜
\(\mathrm{P}\) における \(C_1,~C_2\) の接線が一致するので\(,\) 以下が成り立つ.
① を ② に代入して\(,\) 両辺を \(e^{kb}(>0)\) で割ると\(,\)
を得る. これを ① に代入して\(,\)
\(e^{\frac{1}{2}}>0,~\displaystyle \sqrt{\frac{m}{2k}}>0\) であるから\(,\) 両辺を \(2\) 乗して\(,\)

「両辺を \(2\) 乗する」という操作は一般的には同値ではない変形になるので\(,\) 左辺も右辺も正であることを断ることで\(,\) 同値性が保たれるという主張をしています.
(4) の解答〜面積は(上の式)ー(下の式)〜
求める面積を \(S\) とおくと\(,\)




コメント