問題文全文
放物線 \(y=x^2-2x\) を \(C\) , 直線 \(y=x\) を \(l\) とする. \(C\) と \(l\) の交点のうち, \(x\) 座標が正となるものを \(P\) とする. \(C\) と \(l\) が囲む部分を \(A\) とし, \(A\) を \(y\) 軸の周りに 1 回転して得られる回転体の体積を \(V_1\), \(A\) を \(x\) 軸の周りに 1 回転して得られる回転体の体積を \(V_2\) とする.
(1) \(P\) の座標を求めよ.
(2) \(A\) の面積を求めよ.
(3) \(V_1\) を求めよ.
(4) \(V_2\) を求めよ.
(1),(2)の解答
(1) は連立するだけ, \(2\) は 2 次関数と直線で囲まれる部分の面積ですからいわゆる\(\displaystyle\frac{1}{6}\) 公式です.
(1) \(x^2-2x=x\)より, \(x(x-3)=0\) であるから, \(x=0, 3.\)
\(x>0\) より, \(x=3.\) よって, \(P(3, 3).\)
(2) \(A\) の面積を \(S\) とおくと,
(3)の着眼点
\(y\) 軸回転の問題です. まず注目したいのは領域 \(A\) が \(y\) 軸をまたがっていないことです. またがっていたら折り返しを考えないといけなくなるので大変ですが, またがっていないものは容易に求めることができます.
合言葉は『\(y=t\) で切って「右ー左」』です. 直線 \(y=t\) を \(-1\leqq t\leqq 3\) の範囲で動かすとき右側の交点が作る円から左側の交点が作る円をくり抜いてドーナツを作るイメージです. (\(\left(0,t\right)\)を中心とする同心円です)そして各 \(t\) で作ったドーナツを積み重ねることで求めたい体積にするというイメージができればOKです.
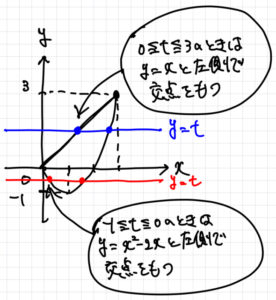
上図を見ればわかりますが \(-1\leqq t\leqq 0\) のときと, \(0\leqq t\leqq 3\) のときで左側にある曲線が変わるので注意が必要です.
(3)の解答
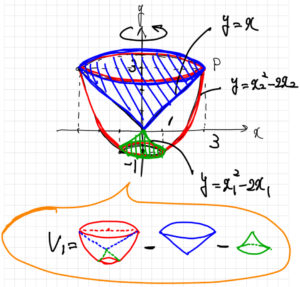
\(y=x^2-2x\) を \(0\leqq x_1\leqq 1\) の部分と\(1\leqq x_2\leqq 3\) の部分に分ける.
求める体積 \(V_1\) は \(y=x_2^2-2x_2\) を \(y\) 軸の周りに回転させた立体(上図の赤い立体)の体積から, \(y=x\) を \(0\leqq x\leqq 3\) の範囲で \(y\) 軸の周りに回転させた立体(上図の青い円錐)の体積と, \(y=x_1^2-2x_1\) を \(y\) 軸の周りに回転させた立体(上図の緑の立体)の体積を除いたものである.
(4)の着眼点
(4)に関しては, \(x\) 軸をまたがってしまっているので, \(x\) 軸で折り返して重なる部分を回転させる必要があります.
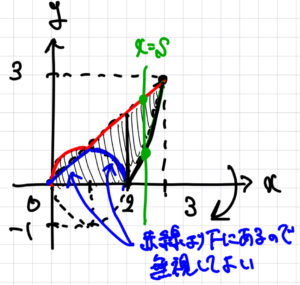
\(x\) 軸に関して折り返すと上図のようになります.このとき, 青線の部分は赤線よりも下にあるため, \(x\) 軸に関して回転させたときに内包されてしまうため考える必要はありません.
実質, \(0\leqq x\leqq 2\) に関しては赤色部分の回転体の体積を求め, \(2\leqq x \leqq 3\) の部分に関しては, 赤色部分の回転体の体積から, 黒色部分の回転体の体積をくり抜くことで求めることができます.
(4)の解答
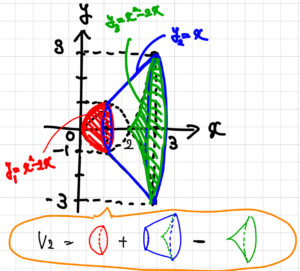
上図のように, \(0\leqq x\leqq 1\) における放物線(上図の赤い曲線)を \(y_1=x^2-2x\), \(1\leqq x\leqq 3\) における直線(上図の青い直線)を \(y_2=x\), \(2\leqq x\leqq 3\) における放物線(上図の緑色の曲線)を \(y_3=x^2-2x\) とおく.
求める体積 \(V_2\) は \(y_1\) を \(x\) 軸の周りに回転させた立体(図の赤色の立体)と \(y_2\)を \(x\) 軸の周りに回転させた円錐台(図の青色の円錐台)を合わせた体積から \(y_3\) を \(x\)軸の周りに回転させた立体(図の緑色の立体)の体積を除いたものである.
難易度は入試基礎だと思われるので確実に得点しておきたいところです.



