2月6日に理工学部の入試が行われました. 受験された方はお疲れさまでした. 微積分以外の問題についてはtwitterにて解答速報を発信していますので合わせてご覧いただけますと幸いです.
問題文全文
関数 \(f(x)\) を \(f(x)=|x\sin x|\) で定める.
(1) \(x\sin x\) の導関数 \((x\sin x)^{\prime}\) と不定積分 \(\displaystyle \int x\sin xdx\) を求めよ.
座標平面において\(,\) 原点 \(\mathrm{O}\) から曲線 \(y=f(x)\) に傾きが正の接線を引く. その接点の \(x\) 座標を小さい順に
\begin{align}x_0,~x_1,~x_2,~\cdots \cdots,~x_n,~\cdots \cdots\end{align}
とおき\(,\)
\begin{align}I_n=\int_{x_{2n}}^{x_{2n+1}}f(x)dx~~(n=0,~1,~2,~\cdots \cdots)\end{align}
とおく.
(2) \(x_n\) を求めよ.
(3) \(I_n\) を求めよ.
(4) \(\displaystyle \sum_{n=0}^{\infty}\frac{1}{I_nI_{n+1}}\) を求めよ.
(1) の解答
\begin{align}(x\sin x)^{\prime}=\sin x+x\cos x~~~~\cdots \fbox{答}\end{align}
\begin{align}x\sin xdx=-x\cos x+\int \cos xdx=-x\cos x+\sin x+C~~~~\cdots \fbox{答}\end{align}
(2) の解答
\(0\) 以上の整数 \(n\) に対して\(,\) \(n\pi <x<(n+1)\pi\) のとき\(,\)
\begin{align}f(x)=\pm x\sin x\end{align}
\((x_n,~f(x_n))\) における接線の方程式は\(,\)
\begin{align}y=\pm (\sin{x_n}+x_n\cos{x_n})(x-x_n)\pm x_n\sin{x_n}\end{align}
原点を通るので\(,\)
\begin{align}0=\mp(\sin{x_n}+x_n\cos{x_n})(x-x_n)\pm x_n\sin{x_n}\end{align}
\begin{align}x_n^2\cos{x_n}=0\end{align}
\(x_n\neq 0\) より
\begin{align}x_n=\frac{2n+1}{2}\pi~~~~\cdots~~ \fbox{答}\end{align}

quandle
\(\cos{x_n}=0\) となるのは\(,\)
\begin{align}x_n=\frac{\pi}{2},~\frac{3\pi}{2},~\frac{5\pi}{2},~\cdots\end{align}
つまり\(,\) 「\(2\) 分の奇数 \(\pi\)」のときです.
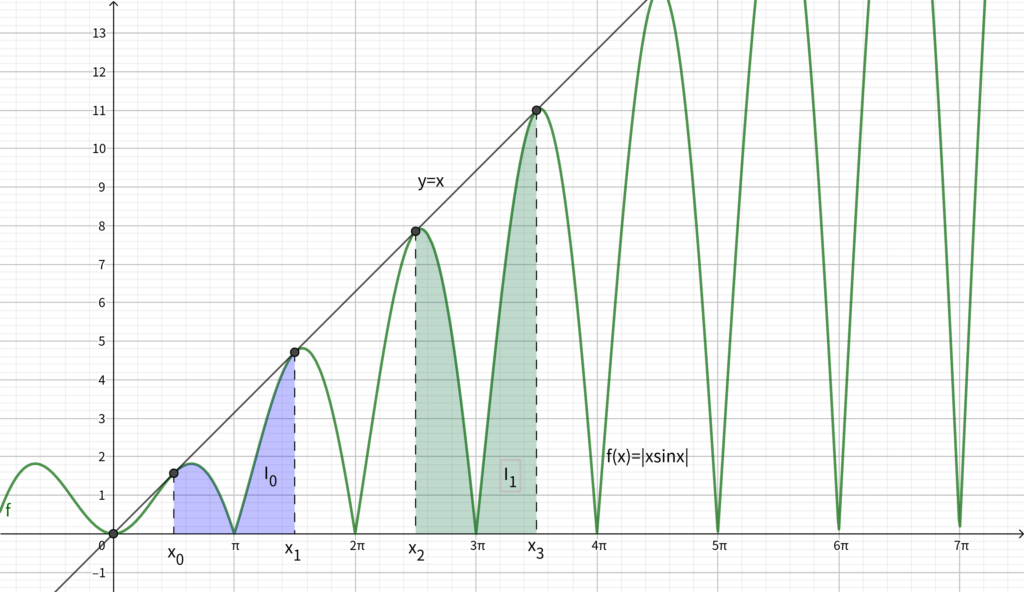
ちなみにこのとき接線は \(y=x\) となります. (下図参照)
(3) の着眼点
\(f(x)=|x\sin x|\) のグラフは下図のように山がいくつも連なるようなものになります.
\(I_n\) は \(x_{2n}\) から \(x_{2n+1}\) までの積分です. \(x_{2n}\) は奇数個目の山の中にあり\(,\) \(x_{2n+1}\) は偶数個目の山の中にあります.
偶数個目の山はもともと \(x\) 軸より下にあったものが絶対値により \(x\) 軸に関して折り返されたものですので積分するときはマイナスをつけないといけないことに注意が必要です.
(3) の解答
\begin{align}I_n=\int_{x_{2n}}^{(2n+1)\pi}x\sin xdx-\int_{(2n+1)\pi}^{x_{2n+1}}x\sin xdx\end{align}
\begin{align}=\biggl[-x\cos x+\sin x\biggr]_{x_{2n}}^{(2n+1)\pi}-\biggl[-x\cos x+\sin x\biggr]_{(2n+1)\pi}^{x_{2n+1}}\end{align}
\begin{align}=(2n+1)\pi-\sin{x_{2n}}-\sin{x_{2n+1}}+(2n+1)\pi\end{align}

quandle
「コサイン奇数 \(\pi\) は \(-1\)」であることと「サイン整数 \(\pi\) は \(0\) 」であることを使っています.
\begin{align}=2(2n+1)\pi-1+1=2(2n+1)\pi~~~~\cdots ~~\fbox{答}\end{align}

quandle
ちゃんとやっておくと\(,\)
\begin{align}\sin{x_{2n}}=\sin{\frac{4n+1}{2}\pi}=\sin{\frac{\pi}{2}+2n\pi}=\sin{\frac{\pi}{2}}=1\end{align}
\begin{align}\sin{x_{2n+1}}=\sin{\frac{2(2n+1)+1}{2}\pi}=\sin{\frac{3}{2}\pi +2n\pi}=\sin{\frac{3}{2}\pi}=-1\end{align}
(4) の解答
\begin{align}\sum_{n=0}^{\infty}\frac{1}{I_nI_{n+1}}=\frac{1}{4{\pi}^2}\sum_{n=0}^{\infty}\frac{1}{(2n+1)(2n+3)}\end{align}

quandle
無限級数 \(\displaystyle \sum_{n=0}^{\infty}\) は部分和の極限 \(\displaystyle \lim_{n\to \infty}\sum_{k=0}^n\) と書き直せます.
\begin{align}=\frac{1}{8{\pi}^2}\lim_{n\to \infty}\sum_{k=0}^n\left(\frac{1}{2k+1}-\frac{1}{2k+3}\right)\end{align}
\begin{align}=\frac{1}{8{\pi}^2}\lim_{n\to \infty}\left(1-\frac{1}{2n+3}\right)=\frac{1}{8{\pi}^2}~~~~\cdots~~\fbox{答}\end{align}

quandle
「\(k\) の差が \(1\)」のときは最初と最後だけが残りますね.









2022年第1問3-2-120x68.jpg)
コメント