理工学部（建築・先化・電電・機械工・土木工）2022年第３問の問題文全文
\(a,~b\) を定数とし\(,\) \(a>1\) かつ \(b>1\) とする. 関数 \(f(x),~g(x)\) を
と定義する. \(f(x)\) は \(x=1\) で極値をとるとする. \(e\) は自然対数の底を表すものとして以下の問いに答えよ.
(1) \(b\) を\(,\) \(a\) を用いて表せ.
(2) 座標平面において\(,\) 曲線 \(y=f(x)\) と曲線 \(y=g(x)\) の交点の座標を\(,\) \(a\) を用いて表せ.
(3) 座標平面において\(,\) 曲線 \(y=f(x)\)\(,\) 曲線 \(y=g(x)\) と \(y\) 軸で囲まれた図形の面積 \(S\) を\(,\) \(a\) を用いて表せ.
(4) (3) で求めた面積 \(S\) が \(9e-18\) となるときの \(a\) の値を求め\(,\) そのときの \(f(1)\) の値を求めよ.
(1) の解答〜十分条件のチェックを忘れずに！〜
\(x=1\) で極値をとるので\(,\) \(f^{\prime}(1)=0\) より\(,\)
\(a>1,~b>1\) より\(,\) \(a-1\neq 0,~b\neq 0\) であるから\(,\)
これはあくまでも極値の候補にすぎません. \(f^{\prime}(x)\) に符号の変化が起こっているかを確認する必要があります. 増減表を作成するのがお手軽です.
このとき\(,\) 増減表は以下のようになる.
増減表より\(,\) 確かに \(x=1\) で極大値をとる.
補足：\(f(x)\) が極値をとるための必要十分条件
点 \((a, f(a))\) が曲線 y=f(x)の極値であるための必要十分条件は\(,\) 以下の \(2\) つを満たすこと.
① \(f^{\prime}(a)=0\)
② \(x=a\) のまわりで \(f′(x)\) の符号が変化する
①を満たす \(a\) を求めると\(,\) 極値の候補が絞られます. それぞれの \(a\) について②を満たしているかのチェックを行いましょう. 今回の問題は 最初から候補が \(1\) しかありませんが\(,\) 必ず②のチェックを行うようにしましょう.
(2) の解答〜交点と言われたら連立方程式を解く〜
\(b^x>0\) より\(,\)
よって\(,\) 交点の座標は\(,\)
(3) の解答〜 \(f(x)\) と \(g(x)\) の位置関係を把握する〜
(2) より\(,\) \(y=f(x)\) と \(y=g(x)\) は \(x=a-1(>0)\) で交点をもつ.
\(x<a-1\) のとき\(,\) \(a-x>1\) より\(,\) \(f(x)>g(x)\) であり\(,\) \(x>a-1\) のとき\(,\) \(a-x<1\) より\(,\) \(f(x)<g(x)\) であるから\(,\) \(y=f(x)\) と \(y=g(x)\) のグラフの位置関係は下図のようになる.
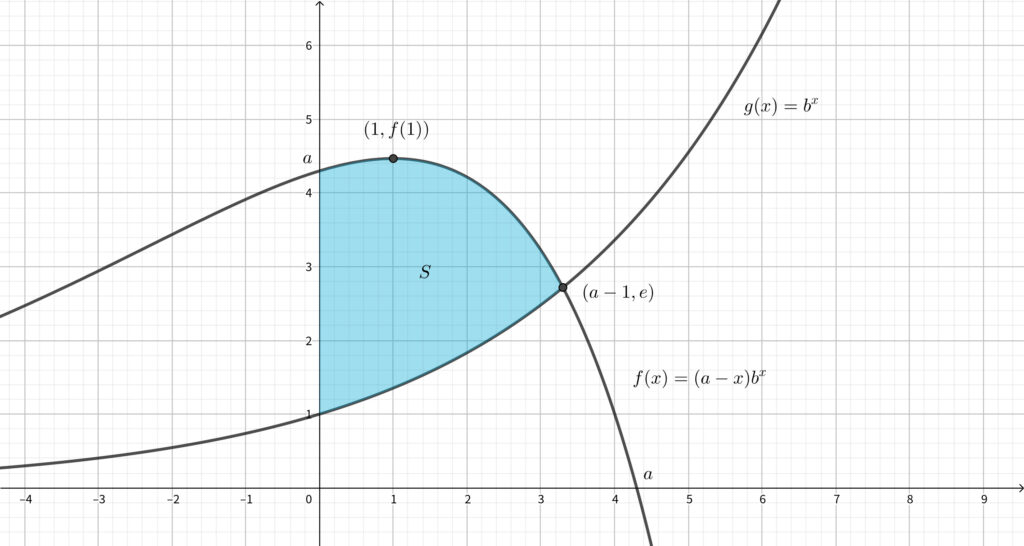
求める面積 \(S\) は
\(\displaystyle b=e^{\frac{1}{a-1}}\) より\(,\)
(4) の解答〜ボーナス問題です。確実に！〜
\(S=9e-18=9(e-2)\) より\(,\)
\(a>1\) より\(,\) \(a-1>0\) であるから\(,\)
このとき\(,\)
コメント