理工学部（建築・先化・電電・機械・土木）2020年第１問（１）

問題文全文

\(x≥0\) で定義された関数 \(f(x)\) を

で定める. ただし, \(e\) は自然対数の底とする.

なので \(f(x)\) は

において最大値をとる. ただし, \(f^{\prime}(x)\) は \(f(x)\) の導関数を表す.

解答

管理人

この問題は微分するだけですので着眼点はありません。積の微分と合成関数の微分をミスなくやってください. 絶対に失点が許されない問題です.

\(e^{-x^2+2\sqrt{2}x}>0\)より, \(f^{\prime}(x)\) と \(-2x^2+2\sqrt{2}x+1\) の符号は一致する.

\(-2x^2+2\sqrt{2}x+1=0\) のとき, \(\displaystyle x=\frac{\sqrt{2}\pm 2}{2}=1\pm\frac{\sqrt{2}}{2}\)

\(x≥0\) における増減表は以下のようになる.

\begin{array}{c|c|c|c|c}x & 0 & \cdots & 1+\frac{\sqrt{2}}{2} & \cdots \\ \hline f^{\prime}(x) & {} & + & 0 & – \\ \hline f(x) & 0 & \nearrow & 極大 & \searrow \\ \end{array}

増減表より, \(\displaystyle 1+\frac{\sqrt{2}}{2}\) のとき最大値をとる.

補足（最小値について）

であることから最小値は \(f(0)=0\) です.

この極限は不定形です. ですが収束値を調べるだけなら（きちんと記述しなくていいのなら）以下のように感覚的に求められます.

分母の \(\displaystyle e^{x^2-2\sqrt{2}x}\) は, \(x\rightarrow \infty\) においては, \(2\sqrt{2}x\) が \(x^2\) に比べて無視できるほどに小さくなりますので \(e^{x^2}\)だと思っていいです.

そして, 分子の \(x\) は分母の \(e^{x^2}\) に比べて無視できるほどに小さくなりますので \(\displaystyle \frac{1}{e^{x^2}}\) だと思っていいです. よって極限値は 0 になります.

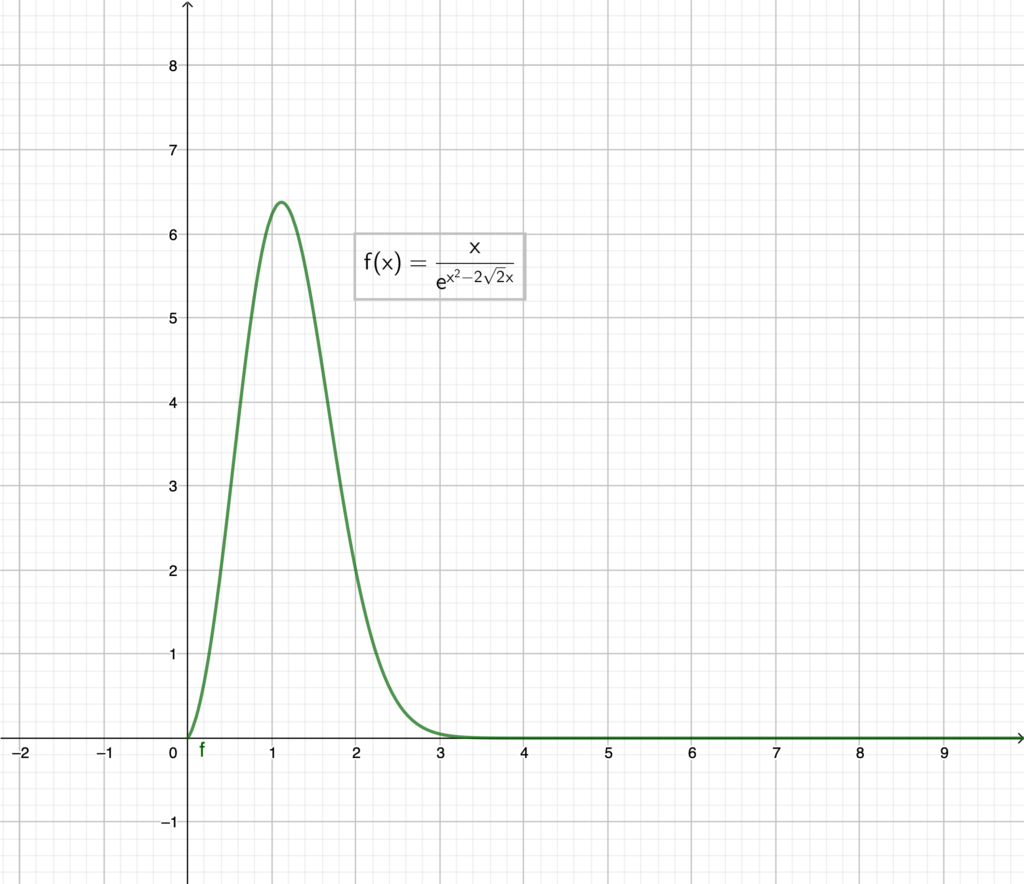
参考までにグラフを描いてみると以下のようになります. だいぶ早い段階で 0 に収束することがわかります.