理学部(数・物・化)2021年第1問(3) の問題文全文
以下の問いに答えよ.
(a) \(f(x)\) は \(3\) 次関数であり\(,\)
\begin{align}f(0)=2,~f(1)=f(2)=f(3)=0\end{align}
を満たすとする. このとき\(,\)
\begin{align}\lim_{x\to \infty}\frac{f(x)}{x^3}=\fbox{$\hskip0.8emあ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\frac{\fbox{$\hskip0.8emニ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emヌ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である. また\(,\) \(f(x)\) の \(x=1\) における微分係数は
\begin{align}f^{\prime}(1)=\fbox{$\hskip0.8emい\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\frac{\fbox{$\hskip0.8emネ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emノ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である.
(b) \(g(x)\) は \(5\) 次関数であり\(,\)
\begin{align}g(1)=g(2)=g(3)=g(4)=g(5)=0,~g(6)=2\end{align}
を満たすとする. このとき\(,\) \(g(x)\) の \(x=4\) における微分係数は
\begin{align}g^{\prime}(4)=\fbox{$\hskip0.8emう\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\frac{\fbox{$\hskip0.8emハ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emヒフ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である. また\(,\)
\begin{align}\int_0^6\{g(x)-g(0)\}dx=\fbox{$\hskip0.8emえ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\fbox{$\hskip0.8emヘホ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
である.
(a) の着眼点〜因数定理の利用〜
\(f(x)\) は \(3\) 次関数とありますから\(,\) 通常は
\begin{align}f(x)=ax^3+bx^2+cx+d~(a\neq 0)\end{align}
と \(4\) つの未知数で表されます. 今回は
\begin{align}f(1)=f(2)=f(3)=0\end{align}
という条件がありますから\(,\) 因数定理より
\begin{align}f(x)=a(x-1)(x-2)(x-3)\end{align}
と未知数 \(1\) つで表すことができます. あとは \(f(0)=2\) を使って \(a\) を決めればOKです!
その後の極限値や微分係数の問題は \(f(x)\) を因数分解したままの形で使うと計算量が抑えられます. むやみに展開しないようにしましょう.
(a) の解答〜微分係数の定義〜
\(f(1)=f(2)=f(3)=0\) より\(,\) 求める \(3\) 次関数は
\begin{align}f(x)=a(x-1)(x-2)(x-3)~~(a\neq 0)\end{align}
とおける. \(f(0)=2\) より\(,\) \(\displaystyle -6a=2\Leftrightarrow a=-\frac{1}{3}\).
よって\(,\)
\begin{align}f(x)=-\frac{1}{3}(x-1)(x-2)(x-3)\end{align}
このとき\(,\)
\begin{align}\lim_{x\to \infty}\frac{f(x)}{x^3}=\lim_{x\to \infty}-\frac{1}{3}\left(1-\frac{1}{x}\right)\left(1-\frac{2}{x}\right)\left(1-\frac{3}{x}\right)=-\frac{1}{3}.\end{align}
また\(,\)
\begin{align}f^{\prime}(1)=\lim_{h\to 0}\frac{f(1+h)-f(1)}{h}\end{align}
\begin{align}=\lim_{h\to 0}-\frac{1}{3}(h-1)(h-2)=-\frac{2}{3}.\end{align}

quandle
思考停止で 「\(f(x)\) を微分して \(x=1\) を代入」としないようにしましょう. 微分係数の定義式を用いることで因数分解した形がうまく活用できます.
あ:ー ニ:1 ヌ:3 い:ー ネ:2 ノ:3
(b) の着眼点〜平行移動して考える〜
\(g^{\prime}(4)\) を求めるところまでは (a) と同様の手順でいけそうです.
後半の \(\displaystyle \int_0^6\{g(x)-g(0)\}dx\) をどうするかを考えていきます.
私がこの問題を考えるとき\(,\) 最初は \(g(x)-g(0)\) という形に注目して「平均値の定理」の利用を考えました. ですがうまい変形が見つからず断念しました.
やはり今回は \(g(x)\) が因数分解の形でかけていることに注目すべきです.
\begin{align}g(x)=b(x-1)(x-2)(x-3)(x-4)(x-5)\end{align}
という形をしていることと\(,\) 積分範囲が \(0\leqq x\leqq 6\) であることに注目します. 積分の値は面積ですから\(,\) 平行移動してもその値は変わりません.
そこで\(,\) \(g(x)\) のグラフを \(x\) 軸方向に \(-3\) 平行移動すると\(,\)
\begin{align}g(x+3)=b(x+2)(x+1)x(x-1)(x-2)\end{align}
と対称性のある形で表され\(,\) かつ\(,\) 積分範囲も \(-3\leqq x\leqq 3\) となり奇関数・偶関数の積分公式が使えそうです.
奇関数・偶関数の積分公式については以下でまとめていますのでご参照ください.
(b) の解答〜奇関数・偶関数の積分公式〜
\(g(1)=g(2)=g(3)=g(4)=g(5)=0\) より\(,\) 求める \(5\) 次関数 \(g(x)\) は
\begin{align}g(x)=b(x-1)(x-2)(x-3)(x-4)(x-5)~~(b\neq 0)\end{align}
とおける. \(g(6)=2\) より\(,\) \(\displaystyle 120b=2\Leftrightarrow b=\frac{1}{60}\)
よって\(,\)
\begin{align}g(x)=\frac{1}{60}(x-1)(x-2)(x-3)(x-4)(x-5)\end{align}
このとき\(,\)
\begin{align}g^{\prime}(4)=\lim_{h\to 0}\frac{g(4+h)-g(4)}{h}\end{align}
\begin{align}=\lim_{h\to 0}\frac{1}{60}(h+3)(h+2)(h+1)(h-1)=-\frac{1}{10}.\end{align}
また \(,\)
\begin{align}\int_0^6\{g(x)-g(0)\}dx=\int_{-3}^3\{g(x+3)-g(0)\}dx\end{align}
\begin{align}=\int_{-3}^3\left\{\frac{1}{60}(x+2)(x+1)x(x-1)(x-2)+2\right\}dx\end{align}

quandle
\(\displaystyle h(x)=\frac{1}{60}(x+2)(x+1)x(x-1)(x-2)\) は奇関数です.
\begin{align} h(-x)=\frac{1}{60}(-x+2)(-x+1)(-x)(-x-1)(-x-2)\end{align}
\begin{align}=(-1)^5\frac{1}{60}(x-2)(x-1)x(x+1)(x+2)=-h(x)\end{align}
だからです.
\begin{align}=2\int_0^32dx=4\cdot 3=+12.\end{align}
う:ー ハ:1 ヒ:1 フ:0 え:+ へ:1 ホ:2
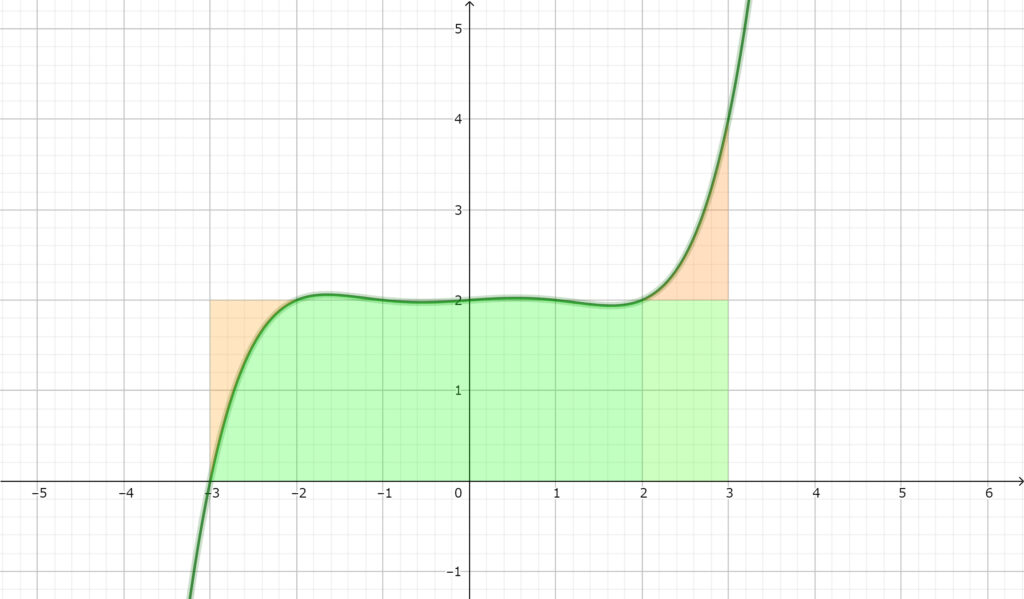
※グラフは以下のようになります. オレンジ色部分を移動させることで\(,\) \(1\times 1\) の正方形が \(12\) 枚分であることが視覚的にも確認できます.
King Property の考え方による別解
\begin{align}I=\int_0^6g(x)dx\end{align}
とおく. \(t=6-x\) とおくと\(,\) \(dt=-dx\) であり\(,\)
\begin{align}\begin{array}{c|c}x & 0 \to 6 \\ \hline t & 6\to 0\end{array}\end{align}
であるから\(,\)
\begin{align}I=\int_0^6g(x)dx\end{align}
\begin{align}=\int_6^0g(6-t)(-dt)=\int_0^6g(6-t)dt\end{align}
\begin{align}=\int_0^6\frac{1}{60}(5-t)(4-t)(3-t)(2-t)(1-t)dt\end{align}
\begin{align}=-\int_0^6\frac{1}{60}(t-1)(t-2)(t-3)(t-4)(t-5)dt\end{align}
\begin{align}=-\int_0^6g(t)dt=-I\end{align}

quandle
\(\displaystyle \int_0^6g(x)dx\) と \(\displaystyle \int_0^6g(t)dt\) は使っている文字が違うだけで全く同じ形をしていますから\(,\) 定積分の値は当然同じになります.
\begin{align}2I=0\end{align}
\begin{align}I=0\end{align}
以上より\(,\)
\begin{align}\int_0^6\{g(x)-g(0)\}dx=I+\int_0^62dx\end{align}
\begin{align}=0+2\cdot 6=+12~~~~\cdots \fbox{答}\end{align}





2021年第1問(3)のコピー.jpg)



コメント
東京理科大学理学部第二部の数学科専用問題も解いていただけませんか?難しい問題ありました
コメントありがとうございます!!ぜひ解きたいので送っていただければと思います!!DMしますね!