東京理科大学理工学部（数・物・情・応生・経営工）2021年第３問| 理科大の微積分

理工学部（数・物・情・応生・経営工）2021年第３問の問題文全文
(1) の解答〜平行移動〜
(2) の着眼点〜連立方程式が解を持たない〜
(2) の解答〜判別式は使えない〜
(3) の解答〜軌跡を求める〜
1. 補足：(3) の逆が成り立つこと
(4) の解答〜判別式を利用〜
(5) の解答〜\displaystyle \frac{1}{6}\) 公式の利用〜

理工学部（数・物・情・応生・経営工）2021年第３問の問題文全文

座標平面上の曲線 \(y=x^2\) を \(C_1\) とおく.

まず\(,\) 曲線 \(C_1\) を\(,\) \(x\) 軸方向に \(a\)\(,\) \(y\) 軸方向に \(b\) だけ平行移動して得られる曲線を \(C_2\) とする.

(1) 曲線 \(C_2\) を表す方程式を求めよ.

(2) \(C_1\) と \(C_2\) が共有点をもたないための必要十分条件を\(,\) \(a,~b\) を用いて表せ.

次に\(,\) 点 \(\mathrm{A}(s,~t)\) を固定する. 点 \(\mathrm{Q}\) が曲線 \(C_1\) 上を動くとき\(,\) 点 \(\mathrm{A}\) に関して\(,\) 点 \(\mathrm{Q}\) と対称な点 \(\mathrm{P}\) の軌跡を \(C_3\) とする.

(3) 曲線 \(C_3\) を表す方程式を求めよ.

(4) \(C_1\) と \(C_3\) が複数の共有点をもつための必要十分条件を\(,\) \(s,~t\) を用いて表せ.

最後に\(,\) \(a=0,~b=-14,~s=-2,~t=13\) のときを考える.

(5) \(C_1\) と \(C_3\) だけで囲まれる部分の面積を \(S_1\) とおき\(,\) \(C_2\) と \(C_3\) だけで囲まれる部分の面積を \(S_2\) とおく. \(C_1,~C_2,~C_3\) の \(3\) つの曲線で囲まれる部分の面積 \(S_2-S_1\) を求めよ.

(1) の解答〜平行移動〜

\begin{align}C_2~:~y=(x-a)^2+b~~~~\cdots ~~\fbox{答}\end{align}

(2) の着眼点〜連立方程式が解を持たない〜

\(C_1\) と \(C_2\) が「共有点を持たない」ということと連立方程式 \(x^2=(x-a)^2+b\) が「実数解を持たない」ということは同値です. （必要十分条件です）

一般に \(2\) 次方程式が実数解を持たないためには\(,\) その判別式 \(D\) が \(D<0\) となればよいです.

ですが今回は \(2\) 次の項がなくなってしまうので判別式は使えないようです・・・

(2) の解答〜判別式は使えない〜

\(C_1\) と \(C_2\) が共有点を持たないことと\(,\) 連立方程式 \(x^2=(x-a)^2+b\) が実数解を持たないことは必要十分である.

\begin{align}x^2=x^2-2ax+a^2+b\end{align}

\begin{align}2ax=a^2+b\end{align}

\(a\neq 0\) のとき\(,\) 実数解 \(\displaystyle x=\frac{a^2+b}{2a}\) を持つため不適.

よって\(,\)

\begin{align}a=0\end{align}

であり\(,\) このとき等号が成り立たないようにすればよいので\(,\)

\begin{align}b\neq 0\end{align}

よって\(,\) 求める必要十分条件は\(,\)

\begin{align}a=0,~b\neq 0~~~~\cdots ~~\fbox{答}\end{align}

quandle

このとき\(,\) \(C_1,~C_2\) はそれぞれ

\begin{align}C_1~:~y=x^2,~C_2~:~y=x^2+b~(b\neq 0)\end{align}

となるので確かに共有点を持ちませんね.

(3) の解答〜軌跡を求める〜

\(\mathrm{Q}(q~,q^2)\) を \(\mathrm{A}\) に関して対称移動した点を \(\mathrm{R}(X,~Y)\) とおく.

線分 \(\mathrm{QR}\) の中点が \(\mathrm{A}\) であるから\(,\)

\begin{align}\frac{q+X}{2}=s~~~~\cdots ①,~\frac{q^2+Y}{2}=t~~~~\cdots ②\end{align}

①より\(,\)

\begin{align}q=2s-X\end{align}

②に代入して\(,\)

\begin{align}(2s-X)^2+Y=2t\end{align}

\begin{align}Y=-(X-2s)^2+2t~~~~\cdots ③\end{align}

逆に\(,\) 放物線 ③ 上の任意の点 \(\mathrm{R}(x,~y)\) は\(,\) 条件を満たす.

quandle

答案としてはこの \(1\) 文を入れておくほうが無難です. そしてこれ以上の説明はいらないかと思います. 一応なぜ逆が成り立つかは後述します.

よって\(,\) 求める軌跡は\(,\)

\begin{align}C_3~:~y=-(x-2s)^2+2t~~~~\cdots ~~\fbox{答}\end{align}

※\(C_3\) の軌跡が描かれる様子は下でシミュレーションできます. A は自由に動かせます.
左下にあるボタンを押すと再生されます.

補足：(3) の逆が成り立つこと

答案としては

逆に\(,\) 放物線 ③ 上の任意の点 \(\mathrm{R}(x,~y)\) は\(,\) 条件を満たす.　

とさえ書いておけば減点されることはなさそうですが\(,\) きちんと論述しておくことにします.

逆に③上の任意の点を \(\mathrm{A}\) に関して対称移動した点が \(y=x^2\) 上にあるということを示せばよいということになります.

＜解答＞\(y=-(x-2s)^2+2t\) 上の任意の点 \(\mathrm{R}(x,~y)\) を点 \(\mathrm{A}\) に関して対称移動した点 \(\mathrm{Q}\) は\(,\)

\begin{align}\overrightarrow{\mathrm{OQ}}=\overrightarrow{\mathrm{OR}}+2\overrightarrow{\mathrm{RA}}\end{align}

\begin{align}=(x,~y)+2(s-x,~t-y)=(2s-x,~2t-y)\end{align}

ここで\(,\) \(q=2s-x\) とおくと\(,\)

\begin{align}2t-y=(x-2s)^2=q^2\end{align}

となり\(,\) \(\mathrm{Q}(q,~q^2)\) とかける. よって \(\mathrm{Q}\) は \(y=x^2\) 上にある.

(4) の解答〜判別式を利用〜

quandle

(2) と同様に\(,\) 共有点をもつことと連立方程式が解をもつことが必要十分であることを利用します. 今回は「複数の」とありますから\(,\) 判別式 \(D\) の符号は \(D>0\) ですね.

\(C_1\) と \(C_3\) が複数の共有点を持つことと\(,\) 連立方程式 \(x^2=-(x-2s)^2+2t\) が異なる実数解を持つことは必要十分である.

\begin{align}x^2=-(x-s)^2+2t\end{align}

\begin{align}x^2=-x^2+4sx-4s^2+2t\end{align}

\begin{align}x^2-2sx+2s^2-t=0\end{align}

判別式を \(D\) とすると \(\displaystyle \frac{D}{4}>0\) より\(,\)

\begin{align}\frac{D}{4}=(-s)^2-(2s^2-t)>0\end{align}

\begin{align}t>s^2~~~~\cdots \fbox{答}\end{align}

(5) の解答〜\displaystyle \frac{1}{6}\) 公式の利用〜

quandle

だいぶ丁寧な誘導がついていますが\(,\) 後半部分の「\(C_1,~C_2,~C_3\) の \(3\) つの曲線で囲まれる部分の面積を求めよ.」とだけ出題されてもおかしくありません. その場合は図を描いて自分で \(S_2-S_1\) であることを見抜かなければなりません.

\(a=0,~b=-14,~s=-2,~t=13\) のとき\(,\)

\begin{align}C_1~:~y=x^2,~C_2~:~y=x^2-14,~C_3~:~y=-(x+4)^2+26\end{align}

\(C_1\) と \(C_3\) の交点の \(x\) 座標は\(,\) 連立方程式 \(x^2=-(x+4)^2+26\) の解であるから\(,\)

\begin{align}x^2=-(x+4)^2+26\end{align}

\begin{align}2x^2+8x-10=0\end{align}

\begin{align}x^2+4x-5=0\end{align}

\begin{align}(x+5)(x-1)=0\end{align}

\begin{align}x=-5,~1\end{align}

また\(,\) \(C_2\) と \(C_3\) の交点の \(x\) 座標は\(,\) 連立方程式 \(x^2-14=-(x+4)^2+26\) の解であるから\(,\)

\begin{align}x^2-14=-(x+4)^2+26\end{align}

\begin{align}2x^2+8x-24=0\end{align}

\begin{align}x^2+4x-12=0\end{align}

\begin{align}(x+6)(x-2)=0\end{align}

\begin{align}x=2,~-6\end{align}

よって\(,\) \(C_1,~C_2,~C_3\) の位置関係は下図のようになる.

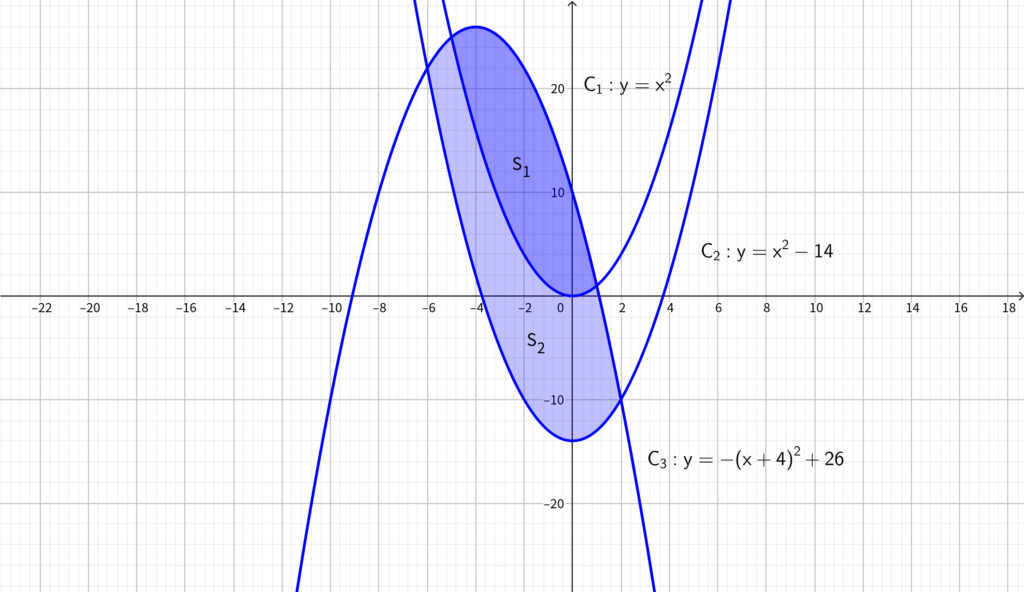
ここで\(,\)

\begin{align}S_1=\int_{-5}^1\{-(x+4)^2+26-x^2\}dx\end{align}

\begin{align}=-2\int_{-5}^1(x+5)(x-1)dx\end{align}

\begin{align}=-\frac{-2}{6}\cdot 6^3=72\end{align}

\begin{align}S_2=\int_{-6}^2\{-(x+4)^2+26-(x^2-14)\}dx\end{align}

\begin{align}=-2\int_{-6}^2(x-2)(x+6)dx\end{align}

\begin{align}=-\frac{-2}{6}\cdot 8^3=\frac{512}{3}\end{align}

であるから\(,\) 求める面積は

\begin{align}S_2-S_1=\frac{512}{3}-72\end{align}

\begin{align}=\frac{512-216}{3}=\frac{296}{3}~~~~\cdots \fbox{答}\end{align}

quandle

\(S_1\) も \(S_2\) も「放物線と放物線」で囲まれる面積ですから\(,\) \(\displaystyle \frac{1}{6}\) 公式を利用できること前提に式変形しましょう.

\(\displaystyle \frac{1}{6}\) 公式については以下でまとめていますので参考にしてください.

1/6公式まとめ

1/6公式についてまとめました。使いこなせば面積計算がかなり速くなります。理科大の過去問を使って練習できるようになっているのでぜひ挑戦してみてください。