3 月 4 日に理学部第二部の入試が行われました. 理科大は日本で唯一理学部の夜間が設置されている大学です. 仕事をしながら学業にも励みたい社会人の方などにおすすめです.
微積分以外の問題についてはtwitterで解答速報をあげていますので\(,\) ご興味のある方はそちらも合わせて見ていただけますと幸いです.
問題文全文
(1) \(a,~b\) を異なる実数とする. \(0\) 以上の整数 \(m,~n\) に対し\(,\)
\begin{align}I(m,~n)=\int_a^b(x-a)^m(b-x)^ndx\end{align}
と定める. このとき
\begin{align}\frac{I(9,~4)}{I(10,~3)}=\frac{\fbox{$\hskip0.8emリ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emル\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である.
(2) \(0\) 以上の整数 \(m,~n\) に対し\(,\)
\begin{align}J(m,~n)=\int_{\frac{3}{2}}^{\frac{7}{2}}\left(x-\frac{3}{2}\right)^m\left(\frac{7}{2}-x\right)^ndx\end{align}
と定める. このとき \(\displaystyle J(3,~0)=\fbox{$\hskip0.8emレ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~,~\frac{J(2,~1)}{J(3,~0)}=\frac{\fbox{$\hskip0.8emロ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emヮ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) であるので\(,\)
\begin{align}J(2,~1)=\frac{\fbox{$\hskip0.8emヲ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emン\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
となる.
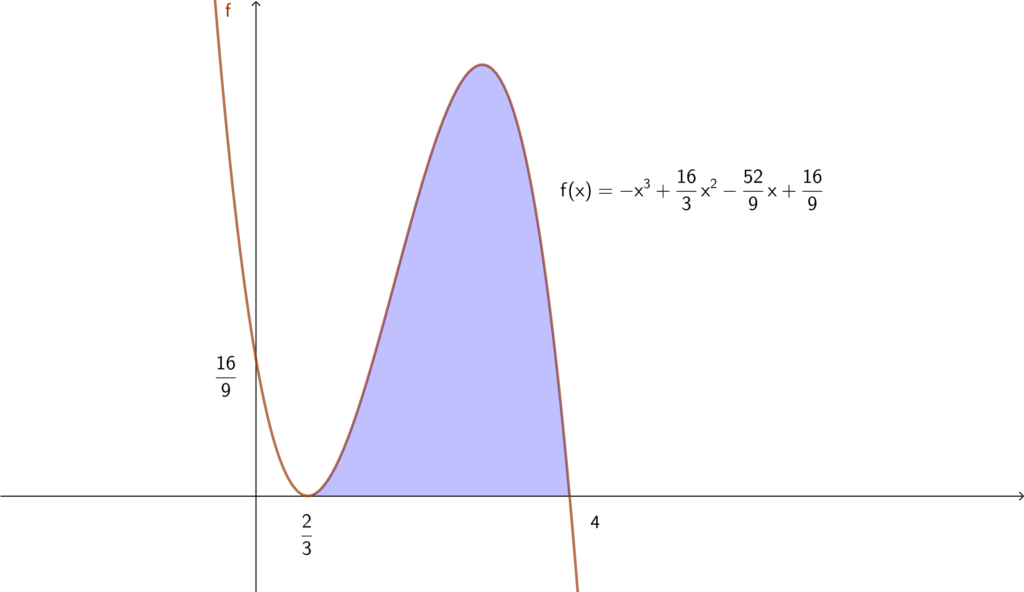
(3) 関数 \(f(x)\) を
\begin{align}f(x)=-x^3+\frac{16}{3}x^2-\frac{52}{9}x+\frac{16}{9}\end{align}
と定める. \(f(x)=0\) をみたす \(x\) のなかで\(,\) 最小なものを \(a\)\(,\) 最大なものを \(b\) とすると\(,\) \(\displaystyle a=\frac{\fbox{$\hskip0.8emあ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emい\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~,~b=\fbox{$\hskip0.8emう\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である. また\(,\)
\begin{align}\int_a^bf(x)dx=\frac{\fbox{$\hskip0.8emえおかき\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emくけこ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である.
(1) の着眼点
\(I(9,~4)\) と \(I(10,~3)\) の比を聞かれています. 比を聞かれるときはだいたい約分ができる形であることが多いです.
また\(,\) 被積分関数が積の形をしている積分漸化式の問題のようですから部分積分を使うことは間違いなさそうです.
部分積分ではどちらを後で微分するのかを選ぶ必要があります. \(9\rightarrow 10,~4\rightarrow 3\) となっていることに注目すれば\(,\) \((b-x)^n\) の方をあとで微分すればいいということが予想できます.
(1) の解答
\begin{align}I(m,~n)=\int_a^b(x-a)^m(b-x)^ndx\end{align}
\begin{align}=\biggl[\frac{1}{m+1}(x-a)^{m+1}(b-x)^n\biggr]_a^b-\int_a^b\frac{1}{m+1}(x-a)^{m+1}\cdot n(b-x)^{n-1}\cdot (-1)dx\end{align}
\begin{align}=\frac{n}{m+1}\int_a^b(x-a)^{m+1}(b-x)^{n-1}dx=\frac{n}{m+1}I(m+1,~n-1)\end{align}
\begin{align}\frac{I(m,~n)}{I(m+1,~n-1)}=\frac{n}{m+1}\end{align}
\(m=9,~n=4\) を代入して\(,\)
\begin{align}\frac{I(9,~4)}{I(10,~3)}=\frac{4}{9+1}=\frac{2}{5}~~~~\cdots \fbox{答}\end{align}
リ:2 ル:5
(2) の着眼点
\(J(m,~n)\) と \(I(m,~n)\) の関係に注目します.
すぐに \(I(m,~n)\) に \(\displaystyle a=\frac{3}{2},~b=\frac{7}{2}\) を代入したものであることが分かります.
そして\(,\) (1) で求めた \(I(m,~n)\) と \(I(m+1,~n-1)\) の関係式には\(,\) \(a,~b\) の文字が含まれていないことから\(,\) \(a,~b\) のとり方によらないことが分かります.
つまり \(J(m,~n)\) においても \(I(m,~n)\) とまったく同じ漸化式が得られるはずです.
(2) の解答
\begin{align}J(3,~0)=\int_{\frac{3}{2}}^{\frac{7}{2}}\left(x-\frac{3}{2}\right)^3dx\end{align}
\begin{align}=\biggl[\frac{1}{4}\left(x-\frac{3}{2}\right)^4\biggr]_{\frac{3}{2}}^{\frac{7}{2}}=4~~~~\cdots \fbox{答}\end{align}
\(J(m,~n)\) は \(I(m,~n)\) の \(\displaystyle a=\frac{3}{2},~b=\frac{7}{2}\) のときと等しく\(,\) (1) より \(I(m,~n)\) と \(I(m+1,~n-1)\) の関係は \(a,~b\) によらないので\(,\)
\begin{align}\frac{J(m,~n)}{J(m+1,~n-1)}\left(=\frac{I(m,~n)}{I(m+1,~n-1)}\right)=\frac{n}{m+1}\end{align}
よって\(,\)
\begin{align}\frac{J(2,~1)}{J(3,~0)}=\frac{1}{2+1}=\frac{1}{3}~~~~\cdots \fbox{答}\end{align}
したがって\(,\)
\begin{align}J(2,~1)=\frac{1}{3}\cdot 4=\frac{4}{3}~~~~\cdots \fbox{答}\end{align}
レ:4 ロ:1 ワ:3 ヲ:4 ン:3
(3) の着眼点
① \(f(x)=0\) は \(3\) 次方程式です. 因数定理による因数分解を考えます. 今回は穴の形が
\begin{align}a=\frac{\fbox{$\hskip0.8emあ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emい\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~,~b=\fbox{$\hskip0.8emう\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
となっていて\(,\) 整数解を持つことがわかっているので整数解を探すと楽です. 勘のいい方であれば\(,\) \(\displaystyle \frac{16}{9}\) という定数項を見ていきなり \(\displaystyle x=\frac{2}{3}\) を見つけることができるかもしれません.
② 因数分解すると
\begin{align}\int_a^bf(x)dx=\int_{\frac{2}{3}}^4\left(x-\frac{2}{3}\right)^2(4-x)dx\end{align}
となり\(,\) \(I(2,~1)\) を求めればよいことが分かります.
問題の流れを考えれば漸化式を用いて求めるのが自然です. そのために \(I(3,~0)\) を求めましょう.
(3) の解答
\begin{align} f(x)=0\Leftrightarrow \left(x-\frac{2}{3}\right)^2(4-x)=0\end{align}
\begin{align}a=\frac{2}{3},~b=4~~~~\cdots \fbox{答}\end{align}
\begin{align}\int_{\frac{2}{3}}^4\left(x-\frac{2}{3}\right)^2(4-x)dx=I(2,~1)\end{align}
より\(,\) \(I(2,~1)\) を求めれば良い. ここで\(,\)
\begin{align}I(3,~0)=\int_{\frac{2}{3}}^4\left(x-\frac{2}{3}\right)^3dx\end{align}
\begin{align}=\biggl[\frac{1}{4}\left(x-\frac{2}{3}\right)^4\biggr]_{\frac{2}{3}}^4=\frac{2500}{81}\end{align}
であることと\(,\)
\begin{align}\frac{I(2,~1)}{I(3,~0)}=\frac{1}{3}\end{align}
であることより\(,\)
\begin{align}I(2,~1)=\frac{1}{3}\cdot \frac{2500}{81}=\frac{2500}{243}~~~~\cdots \fbox{答}\end{align}
あ:2 い:3 う:4 え:2 お:5 か:0 き:0 く:2 け:4 こ:3
1/12公式について
以下の1/12公式を利用すれば (3) は瞬殺できます.
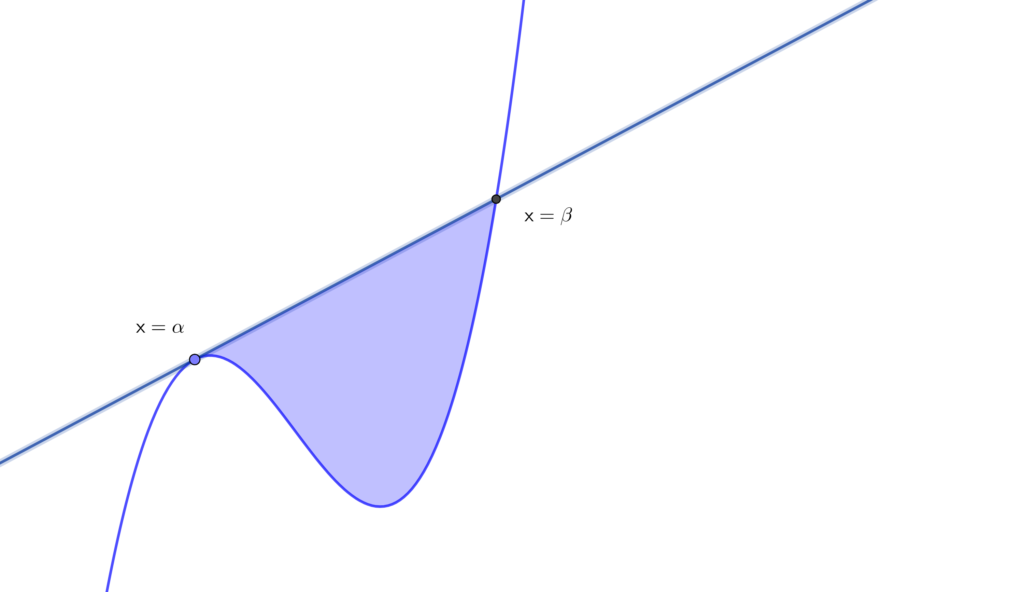
\(\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^2(x-\beta)dx=-\frac{1}{12}(\beta -\alpha)^4\)
この公式は以下のように \(3\) 次関数のグラフと接線によって囲まれる部分の面積を求めたいときに利用します. 穴埋め問題では瞬殺できますのでぜひ知っておいてほしい公式です.
(3) の別解(1/12公式の利用)
\begin{align}\int_{\frac{2}{3}}^4\left(x-\frac{2}{3}\right)^2(4-x)dx\end{align}
\begin{align}=\frac{1}{12}\cdot \left(4-\frac{2}{3}\right)^4=\frac{1}{12}\cdot \left(\frac{10}{3}\right)^4=\frac{2500}{243}~~~~\cdots \fbox{答}\end{align}
※今回の問題の場合は下図の青色部分の面積を求めたことになります.



2022年第1問3-2-120x68.jpg)

コメント