3 月 4 日に理学部第二部の入試が行われました. 受験された方はお疲れさまでした. 微積分以外の問題はtwitterに解答速報をアップしていますので\(,\) よろしければそちらもご覧ください.
問題文全文
(1) 関数 \(f(x)\) を \(f(x)=\sin x-\cos{2x}\) で定め\(,\) \(F(x)\) は \(F^{\prime}(x)=f(x),~F(0)=-1\) をみたす関数とする. ただし\(,\) \(F^{\prime}(x)\) は \(F(x)\) の導関数を表す. \(f(x)=0\) をみたす \(x\) を \(a,~b,~c~(0<a<b<c<2\pi)\) とする. このとき\(,\)
\begin{align}\cos a=\frac{\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~,~\cos b=-\frac{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~,~\cos c=\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
である. また\(,\)
\begin{align}F(a)=-\frac{\fbox{$\hskip0.8emタ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emチ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emツ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~,~F(b)=\frac{\fbox{$\hskip0.8emテ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emト\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emナ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~,~F(c)=\fbox{$\hskip0.8emニ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
である.
(2) \(2\) つの曲線 \(y=\sin x~(0<x<2\pi)\) と \(y=\cos{2x}~(0<x<2\pi)\) で囲まれた \(2\) つの部分の面積の和は
\begin{align}\frac{\fbox{$\hskip0.8emヌ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emネ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emノ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である.
(1) の解答
\begin{align}\sin x-\cos{2x}=0\end{align}
\begin{align}\sin x-(1-2\sin^2x)=0\end{align}
\begin{align}2\sin^2x+\sin x-1=0\end{align}
\begin{align}(\sin x+1)(2\sin x-1)=0\end{align}
\begin{align}\sin x=-1,~\frac{1}{2}\end{align}
\(0<a<b<c<2\pi\) であるから\(,\)
\begin{align}a=\frac{\pi}{6},~b=\frac{5}{6}\pi,~c=\frac{3}{2}\pi\end{align}
よって\(,\)
\begin{align}\cos a=\frac{1}{2}\sqrt{3},~\cos b=-\frac{1}{2}\sqrt{3},~\cos c=0.\end{align}
また\(,\)
\begin{align}F(x)=\int (\sin x-\cos{2x})dx=-\cos x-\frac{1}{2}\sin{2x}+C\end{align}
であり\(,\) \(F(0)=-1\) であることから\(,\)
\begin{align}F(0)=-1+C=-1\end{align}
つまり \(,\)
\begin{align}C=0\end{align}
したがって\(,\)
\begin{align}F(x)=-\cos x-\frac{1}{2}\sin{2x}\end{align}
以上より\(,\)
\begin{align}F(a)=-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{4}=-\frac{3}{4}\sqrt{3},~F(b)=\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{4}=\frac{3}{4}\sqrt{3},~F(c)=0.\end{align}
ケ:1 コ:2 サ:3 シ:1 ス:2 セ:3 ソ:0
タ:3 チ:4 ツ:3 テ:3 ト:4 ナ:3 ニ:0
(2) の着眼点
① 面積を求める問題なので\(,\) \(2\) 曲線の上下関係を調べる必要があります. (1) で \(f(x)=0\) の解を調べていますので\(,\) これがそのまま交点の \(x\) 座標になります.
② 実際の積分計算では (1) で求めた \(F(a),~F(b),~F(c)\) を用いて表すことができるので\(,\) うまく活用して計算量を減らしましょう.
(2) の解答
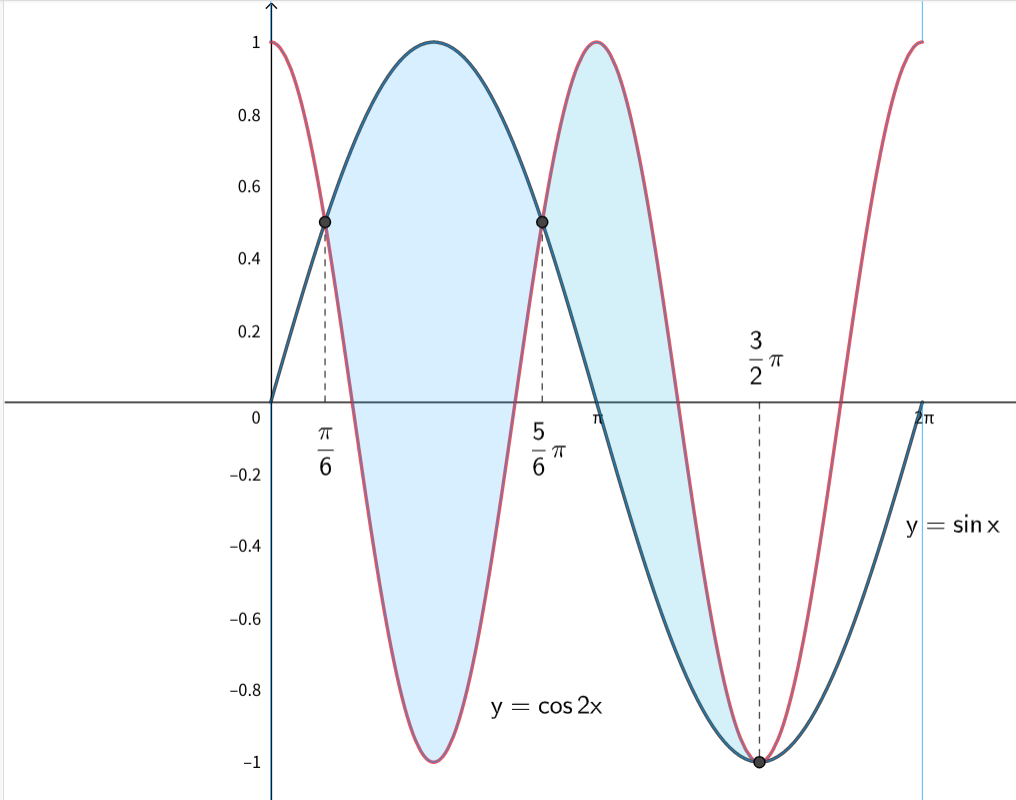
上図のようになるので求める面積を \(S\) とすると\(,\)
\begin{align}S=\int_a^b(\sin x-\cos{2x})dx+\int_b^c(\cos{2x}-\sin x)dx\end{align}
\begin{align}=\biggl[F(x)\biggr]_a^b+\biggl[-F(x)\biggr]_b^c=2F(b)-F(a)-F(c)\end{align}
\begin{align}=\frac{3}{2}\sqrt{3}-\left(-\frac{3}{4}\sqrt{3}\right)-0=\frac{9}{4}\sqrt{3}.\end{align}
ヌ:9 ネ:4 ノ:3





コメント