問題文全文
関数 \(f(x)=x^2+2x\sqrt{1-x^2}~~(-1\leqq x\leqq 1)\) を考える.
(a) \(\displaystyle \int_0^1f(x)dx=\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である.
(b) \(f(x)\) の値域は
\begin{align}\frac{\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}-\sqrt{\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\leqq f(x)\leqq \frac{\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}+\sqrt{\fbox{$\hskip0.8emカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である.
(a) の着眼点
\begin{align}\int_0^12x\sqrt{1-x^2}dx\end{align}
は微分接触型や \(f,~g,~g^{\prime}\) の積分と言われている形です. 具体的には
\begin{align}\int f(g(x))g^{\prime}(x)dx=F(g(x))+C\end{align}
の形の積分のことです. 今回でいうと
\begin{align}f(x)=\sqrt{x},~g(x)=1-x^2\end{align}
の場合ということです. 微分接触型だと判断できたら置換積分などせず一気に積分しましょう.
(a) の解答
\begin{align}\int_0^1f(x)dx=\int_0^1(x^2+2x\sqrt{1-x^2})dx\end{align}
\begin{align}=\biggl[\frac{1}{3}x^3-\frac{2}{3}(1-x^2)^{\frac{3}{2}}\biggr]_0^1=\frac{1}{3}+\frac{2}{3}=1~~~~\cdots \fbox{答}\end{align}

quandle
微分接触系の積分では 頭でやるのは \(f(x)\) の積分だけです.
今回で言えば \(\sqrt{x}\) の積分だけです. この感覚がわかるまでは訓練が必要ですので\(,\) 過去問演習を始めるまでにしっかり鍛えておきましょう.
ア:1
(b) の解答

quandle
値域を聞かれてますから微分して増減表をかいていきます.
\begin{align}(\sqrt{x})^{\prime}=\frac{1}{2\sqrt{x}}\end{align}
は絶対暗記してください. そうでないと合成関数の微分するときに辛いです.
\(-1<x<1\) において\(,\)
\begin{align}f^{\prime}(x)=2x+2\sqrt{1-x^2}+2x\cdot \frac{-2x}{2\sqrt{1-x^2}}\end{align}
\begin{align}=\frac{2x\sqrt{1-x^2}+2(1-x^2)-2x^2}{\sqrt{1-x^2}}=\frac{2(x\sqrt{1-x^2}+1-2x^2)}{\sqrt{1-x^2}}\end{align}

quandle
ここで手が止まると思います. \(f^{\prime}\) の符号を調べるわけですが\(,\) 分母の \(\sqrt{1-x^2}\) は常に正です. よって分子の符号を調べることになります. 考えるべき方法は以下の \(2\) つです.
① \(g(x)=x\sqrt{1-x^2}+1-2x^2\) とおいて\(,\) \(g(x)\) の符号を調べる.
② \(分子=0\) を解いて\(,\) その前後の符号を調べる.
初学者はとりあえず思考停止で②をやりたくなるんですが\(,\) 最初に考えてほしいのは①です. 符号の変化はグラフをかいて考えるべきだからです.
ですが今回の場合は①をやっても計算が煩雑になるばかりでうまくグラフをとらえられません. ですので仕方なく②をやります.
\(f^{\prime}(x)=0\) のとき\(,\)
\begin{align}x\sqrt{1-x^2}=2x^2-1~~~~\cdots (※)\end{align}
両辺を \(2\) 乗して\(,\)
\begin{align}x^2(1-x^2)=4x^4-4x^2+1\end{align}
\begin{align}5x^4-5x^2+1=0\end{align}
\begin{align}x^2=\frac{5\pm \sqrt{5}}{10}\end{align}
\begin{align}x=\pm \sqrt{\frac{5\pm \sqrt{5}}{10}}\end{align}
(※)をみたすのは
\begin{align}x=\sqrt{\frac{5+\sqrt{5}}{10}},~-\sqrt{\frac{5-\sqrt{5}}{10}}\end{align}

quandle
一般に 「\(2\) 乗する」という行為は同値変形ではありません.
出てきた \(x\) の値が(※)をみたすとは限らないため\(,\) 必ず(※)をみたしているかの確認が必要です.
よって増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|}\hline x & -1 & \cdots & \displaystyle -\sqrt{\frac{5-\sqrt{5}}{10}} & \cdots & \displaystyle \sqrt{\frac{5+\sqrt{5}}{10}} & \cdots & 1 \\ \hline f^{\prime}(x) & \times & – & 0 & + & 0 & – & \times \\ \hline f(x) & 1 & \searrow & 極小 & \nearrow & 極大 & \searrow & 1 \\ \hline \end{array} \end{align}
極小値は
\begin{align}f\left(-\sqrt{\frac{5-\sqrt{5}}{10}}\right)=\frac{5-\sqrt{5}}{10}-2\sqrt{\frac{5-\sqrt{5}}{10}}\sqrt{1-\frac{5-\sqrt{5}}{10}}\end{align}
\begin{align}=\frac{5-\sqrt{5}}{10}-2\sqrt{\frac{5-\sqrt{5}}{10}}\sqrt{\frac{5+\sqrt{5}}{10}}=\frac{5-\sqrt{5}}{10}-2\cdot \frac{\sqrt{25-5}}{10}\end{align}
\begin{align}=\frac{5-5\sqrt{5}}{10}=\frac{1-\sqrt{5}}{2}\end{align}
極大値は
\begin{align}f\left(\sqrt{\frac{5+\sqrt{5}}{10}}\right)=\frac{5+\sqrt{5}}{10}+2\sqrt{\frac{5+\sqrt{5}}{10}}\sqrt{1-\frac{5+\sqrt{5}}{10}}\end{align}
\begin{align}=\frac{5+\sqrt{5}}{10}+2\sqrt{\frac{5+\sqrt{5}}{10}}\sqrt{\frac{5-\sqrt{5}}{10}}=\frac{5+\sqrt{5}}{10}+2\cdot \frac{\sqrt{25-5}}{10}\end{align}
\begin{align}=\frac{5+5\sqrt{5}}{10}=\frac{1+\sqrt{5}}{2}\end{align}
よって \(f(x)\) の値域は
\begin{align}\frac{1-\sqrt{5}}{2}\leqq f(x) \leqq \frac{1+\sqrt{5}}{2}~~~~\cdots \fbox{答}\end{align}
イ:1 ウ:5 エ:2 オ:1 カ:5 キ:2
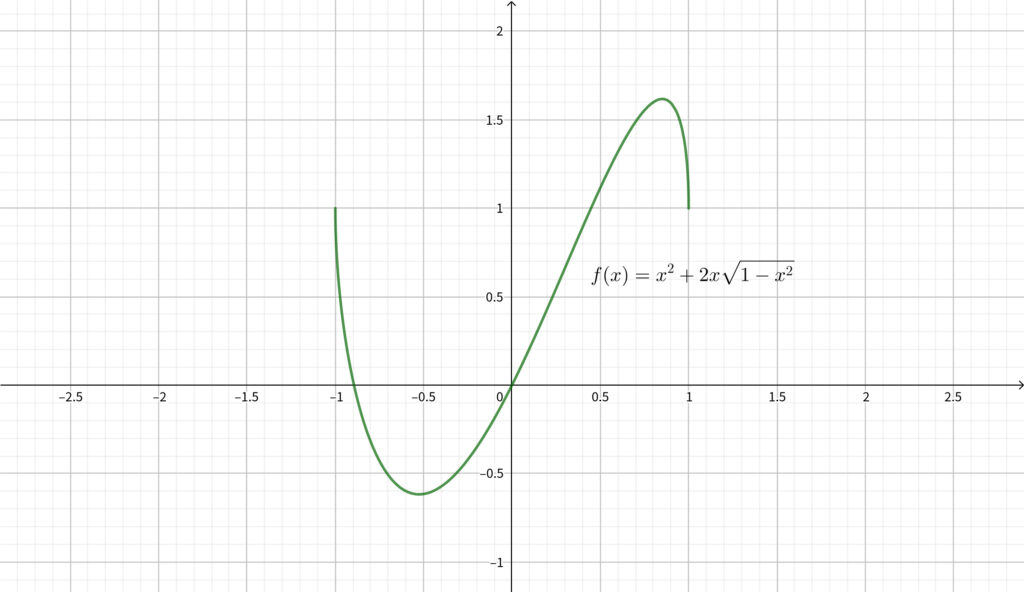
※実際のグラフは下図のようになります









コメント