正の実数 \(x\) に対して定義された関数
\begin{align}f(x)=[\sqrt{x}]+\sqrt{x},~g(x)=2\sqrt{x}-1\end{align}
について考える. ここで\(,\) 実数 \(b\) に対して \(,\) \([b]\) は \(b\) 以下の最大の整数を表す.
関数 \(f(x)\) が連続でない \(x\) の値を小さい順に\(,\) \(a_1,~a_2,~a_3,~\cdots \cdots\) とする. 例えば\(,\) \(a_1=1\) である.
また\(,\) 自然数 \(n\) に対し\(,\) 定義域が \(a_n\leqq x\leqq a_{n+1}\) である関数 \(f_n(x)\) を
\begin{align}f_n(x)=\left\{\begin{array}{cc}f(x) & (a_n \leqq x <a_{n+1}) \\ g(a_{n+1}) & (x=a_{n+1})\end{array}\right.\end{align}
と定める. このとき\(,\) 以下の問いに答えよ.
(1) 自然数 \(n\) に対して\(,\) \(a_n\) を求めよ.
(2) \(x>0\) に対して\(,\) \(g(x)<f(x)\leqq g(x)+1\) を示せ.
(3) 次の値を求めよ.
\begin{align}\sum_{n=1}^6\int_{a_n}^{a_{n+1}}f_n(x)dx\end{align}
(4) \(4\) つの曲線 \(y=f_2(x),~y=f_3(x),~y=g(x),~y=g(x)+1\) で囲まれた図形の面積を求めよ.
(5) \(4\) つの曲線 \(y=f_2(x),~y=f_3(x),~y=g(x),~y=g(x)+1\) で囲まれた図形を \(x\) 軸の周りに \(1\) 回転してできる回転体の体積を求めよ.
(1) の解答
\begin{align}a_n=n^2~~~~\cdots \fbox{答}\end{align}

quandle
ガウス記号[ ]がついた関数は各整数値で不連続なグラフになります.
\(\sqrt{x}\) が整数値を取るのは \(x\) が平方数のときですね.
(2) の解答
\begin{align}g(x)+1-f(x)=\sqrt{x}-[\sqrt{x}]\geqq 0\end{align}
より\(,\)
\begin{align}f(x)\leqq g(x)+1\end{align}

quandle
任意の実数 \(t\) に対して\(,\)
\begin{align}t\geqq [ t ] \end{align}
が成り立ちます. \([ t ]\) は \(t\) の整数部分ですから明らかですね.
\begin{align}f(x)-g(x)=[\sqrt{x}]-\sqrt{x}+1\end{align}
\begin{align}=1-(\sqrt{x}-[\sqrt{x}])>0\end{align}

quandle
\(\sqrt{x}-[\sqrt{x}]\) は \(\sqrt{x}\) の小数部分のことですから \(1\) より小さいですよね.
以上より\(,\)
\begin{align}g(x)<f(x)\leqq g(x)+1\end{align}
(3) の着眼点
この問題はかなり慎重に考えなければなりません. 被積分関数の \(f_n(x)\) が \(x=a_{n+1}\) のときだけ \(g(x)\) を用いて定義されているためです.
被積分関数は積分範囲上で連続な関数でなければなりません. (少なくとも高校範囲では)
記述式でもあるのでここの議論はしておくべきかと思います. 実際の受験生でそこまでやった人はそう多くないとは思いますが.
(3) の解答
関数 \(y=f_n(x)\) が \(a_n\leqq x \leqq a_{n+1}\) で連続であることを示す.
\(a_n\leqq x <a_{n+1}\) つまり \(n^2\leqq x < (n+1)^2\) のとき\(,\)
\begin{align}f_n(x)=f(x)=[\sqrt{x}]+\sqrt{x}=n+\sqrt{x}\end{align}
は 連続である.
次に \(x=a_{n+1}\) における連続性を示す.
\begin{align}\lim_{x\to a_{n+1}-0}f_n(x)=f_n\left(a_{n+1}\right)\end{align}
を示せばよい.
\begin{align}\lim_{x\to a_{n+1}-0}f_n(x)=\lim_{x\to (n+1)^2-0}\left([\sqrt{x}]+\sqrt{x}\right)\end{align}
\begin{align}=n+(n+1)=2n+1\end{align}

quandle
\(x\) が \((n+1)^2\) よりも小さい値をとりますから
\begin{align}\lim_{x\to (n+1)^2-0}[\sqrt{x}]=n\end{align}
となります. ここの判断はとてもむずかしいと思います.
一方\(,\)
\begin{align}f_n\left(a_{n+1}\right)=g\left((n+1)^2\right)=2(n+1)-1=2n+1\end{align}
以上より\(,\) \(x=a_{n+1}\) においても連続.
\begin{align}\sum_{n=1}^6\int_{a_n}^{a_{n+1}}f_n(x)dx=\sum_{n=1}^6\int_{n^2}^{(n+1)^2}(n+\sqrt{x})dx\end{align}
\begin{align}=\sum_{n=1}^6\biggl[nx+\frac{2}{3}x\sqrt{x}\biggr]_{n^2}^{(n+1)^2}=\sum_{n=1}^6\left\{n(n+1)^2-n^3+\frac{2}{3}(n+1)^3-\frac{2}{3}n^3\right\}\end{align}
\begin{align}=\sum_{n=1}^6\left(4n^2+3n+\frac{2}{3}\right)=\frac{2}{3}\cdot 6\cdot 7\cdot 13+\frac{3}{2}\cdot 6\cdot 7+\frac{2}{3}\cdot 6\end{align}
\begin{align}=364+63+4=431~~~~\cdots \fbox{答}\end{align}
(4) の解答
\begin{align}f_2(x)=\left\{\begin{array}{cc}\sqrt{x}+2 & (4\leqq x < 9) \\ 5 & (x=9)\end{array}\right.\end{align}
\begin{align}f_3(x)=\left\{\begin{array}{cc}\sqrt{x}+3 & (9\leqq x < 16) \\ 7 & (x=16)\end{array}\right.\end{align}
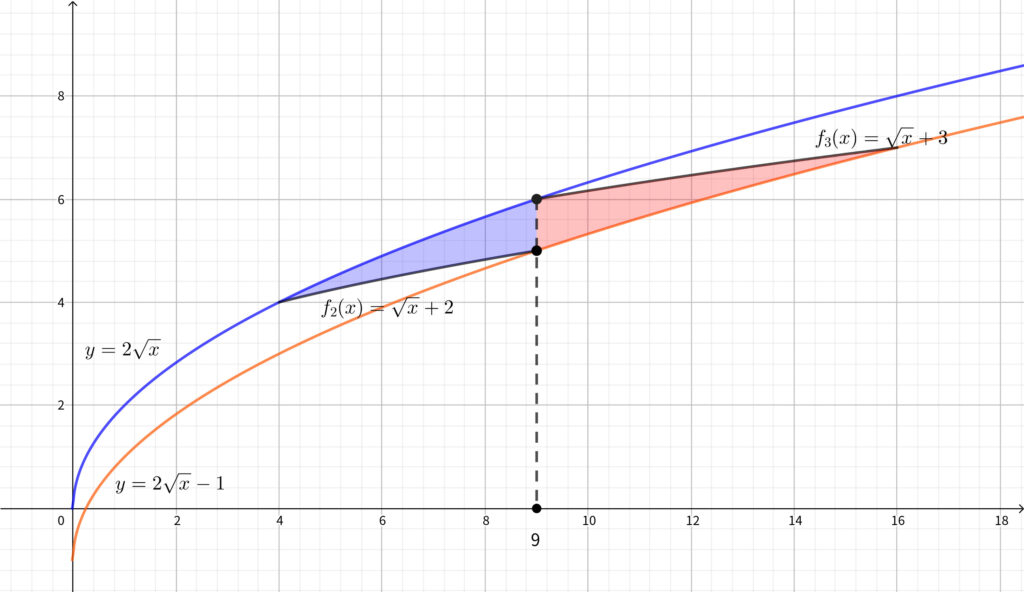
求める面積は上図の青色部分と赤色部分の和である. 求める面積を \(S\) とおくと
\begin{align}S=\int_4^9\{2\sqrt{x}-(2+\sqrt{x})\}dx+\int_9^{16}\{(3+\sqrt{x})-(2\sqrt{x}-1)\}dx\end{align}
\begin{align}=\int_4^9(\sqrt{x}-2)dx+\int_9^{16}(4-\sqrt{x})dx=\biggl[\frac{2}{3}x\sqrt{x}-2x\biggr]_4^9+\biggl[4x-\frac{2}{3}x\sqrt{x}\biggr]_9^{16}\end{align}
\begin{align}=\frac{2}{3}(27-8)-2(9-4)+4(16-9)-\frac{2}{3}(64-27)=6~~~~\cdots \fbox{答}\end{align}
(5) の解答
求める体積を \(V\) とおく.
\begin{align}V=\pi \int_4^9\{(2\sqrt{x})^2-(2+\sqrt{x})^2\}dx+\pi\int_9^{16}\{(3+\sqrt{x})^2-(2\sqrt{2}-1)^2\}dx\end{align}
\begin{align}\frac{V}{\pi}=\int_4^9(3x-4\sqrt{x}-4)dx+\int_9^{16}(-3x+10\sqrt{x}+8)dx\end{align}
\begin{align}=\biggl[\frac{3}{2}x^2-\frac{8}{3}x\sqrt{x}-4x\biggr]_4^9+\biggl[-\frac{3}{2}x^2+\frac{20}{3}x\sqrt{x}+8x\biggr]_9^{16}\end{align}
\begin{align}=\frac{3}{2}(81-16)-\frac{8}{3}(27-8)-4(9-4)-\frac{3}{21}(256-81)+\frac{20}{3}(64-27)+8(16-9)\end{align}
\begin{align}=\frac{195-525}{2}+\frac{740-152}{3}+36=67\end{align}
したがって\(,\)
\begin{align}V=67\pi~~~~\cdots \fbox{答}\end{align}

quandle
体積計算をするときは右辺に何度も \(\pi\) が出てくると煩わしいので\(,\) \(\displaystyle \frac{V}{\pi}\) として計算を進めることをお勧めします. 最後に \(\pi\) 倍するのを忘れないようにしましょう.







2021年第3問.jpg)

2015年第3問のコピー-120x68.jpg)
コメント