問題文全文
\(a\) を実数の定数とし\(,\) \(2\) つの関数 \(f(x),~g(x)\) を
\begin{align}f(x)=-e^{-\frac{x}{2}}+a,~g(x)=e^{\frac{x}{2}}+4e^{-\frac{x}{2}}\end{align}
と定め\(,\) 座標平面上の \(2\) つの曲線 \(y=f(x),~y=g(x)\) を考える. ここで\(,\) \(e\) は
\begin{align}e=\lim_{t\to 0}(1+t)^{\frac{1}{t}}\end{align}
によって定まる実数とする.
(1) \(y=f(x)\) の接線で\(,\) 点 \((4,~a)\) を通るものの方程式は\(,\)
\begin{align}\fbox{$\hskip1.5em(あ)\hskip1.5em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
と書ける.
(2) \(y=f(x)\) と \(y=g(x)\) がただ \(1\) つの共有点 \(\mathrm{P}\) をもつとき\(,\)
\begin{align}a=\fbox{$\hskip1.5em(い)\hskip1.5em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
であり\(,\) その共有点 \(\mathrm{P}\) の座標は\(,\)
\begin{align}\fbox{$\hskip1.5em(う)\hskip1.5em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
である.
(1) の解答
\begin{align}f^{\prime}(x)=\frac{1}{2}e^{-\frac{x}{2}}\end{align}
より\(,\) 接点 の座標を \(\displaystyle \left(t,~-e^{-\frac{t}{2}}+a\right)\) とおくと\(,\) 接線の方程式は
\begin{align}y=\frac{1}{2}e^{-\frac{t}{2}}(x-t)-e^{-\frac{t}{2}}+a\end{align}
\((4,~a)\) を通るので\(,\)
\begin{align}a=\frac{1}{2}e^{-\frac{t}{2}}(4-t)-e^{-\frac{t}{2}}+a\end{align}
\begin{align}\frac{1}{2}(4-t)=1\end{align}
\begin{align}t=2\end{align}
したがって\(,\) 求める接線の方程式は
\begin{align}y=\frac{1}{2e}(x-2)-\frac{1}{e}+a\end{align}
\begin{align}(あ)~~~~y=\frac{1}{2e}x-\frac{2}{e}+a~~~~\cdots \fbox{答}\end{align}
(2) の解答
\begin{align}-e^{-\frac{x}{2}}+a=e^{\frac{x}{2}}+4e^{-\frac{x}{2}}\end{align}
\begin{align}a=e^{\frac{x}{2}}+5e^{-\frac{x}{2}}\end{align}

quandle
この方程式がただ一つの解を持てば\(,\) \(y=f(x)\) と \(y=g(x)\) はただ一つの共有点を持ちます.
右辺を \(h(x)\) とおいて\(,\) 曲線 \(y=h(x)\) と直線 \(y=a\) の共有点がただ一つになるような \(a\) の値を求めましょう. いわゆる「定数分離法」です.
\begin{align}h(x)=e^{\frac{x}{2}}+5e^{-\frac{x}{2}}\end{align}
とおく.
\begin{align}h^{\prime}(x)=\frac{1}{2}e^{\frac{x}{2}}-\frac{5}{2}e^{-\frac{x}{2}}=\frac{1}{2}e^{-\frac{x}{2}}(e^x-5)\end{align}
\(\displaystyle \frac{1}{2}e^{-\frac{x}{2}}>0\) より\(,\) \(y=h^{\prime}(x)\) の増減は \(y=e^x-5\) の増減と一致するので\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|}\hline x & \cdots & \log{5} & \cdots\\ \hline h^{\prime}(x) & – & 0 & + \\ \hline h(x) & \searrow & 2\sqrt{5} & \nearrow \\ \hline \end{array}\end{align}
\begin{align}\lim_{x\to \pm \infty}\left(e^{\frac{x}{2}}+5e^{-\frac{x}{2}}\right)=\infty\end{align}
であることより\(,\)
\begin{align}(い)~~~~a=2\sqrt{5}~~~~\cdots \fbox{答}\end{align}
のとき\(,\) ただ一つの共有点をもつ.
※参考に \(y=h(x)\) のグラフは以下のようになります.
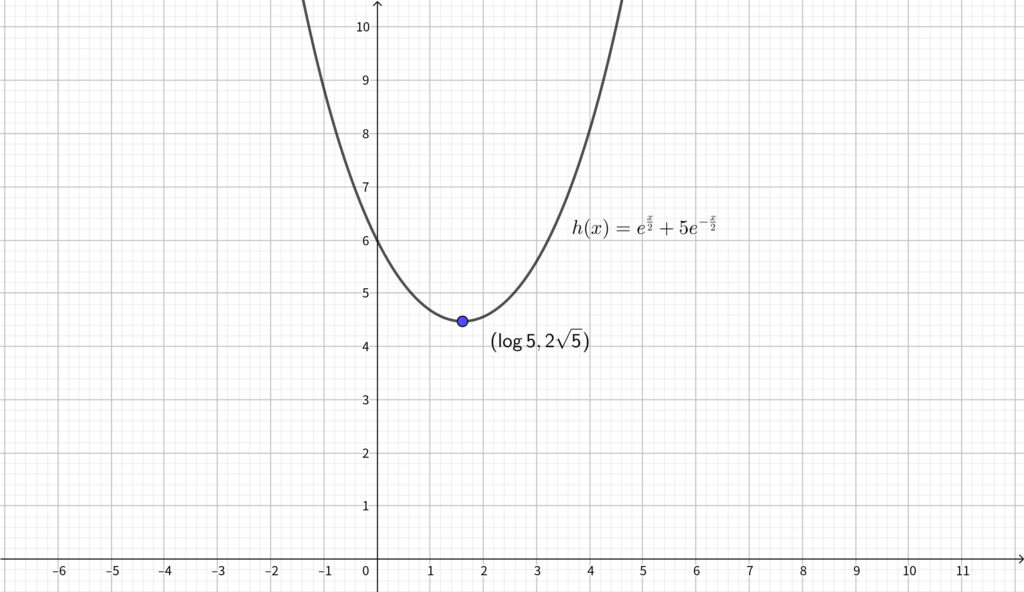
このとき\(,\) 点 \(\mathrm{P}\) の \(y\) 座標は
\begin{align}y=-e^{-\frac{\log{5}}{2}}+2\sqrt{5}=-\frac{1}{\sqrt{5}}+2\sqrt{5}=\frac{9\sqrt{5}}{5}\end{align}

quandle
計算の補足すると
\begin{align}-e^{-\frac{\log{5}}{2}}=-\left(e^{\log{5}}\right)^{-\frac{1}{2}}=-5^{-\frac{1}{2}}=-\frac{1}{\sqrt{5}}\end{align}
と変形しています.
\begin{align}(う)~~~~\mathrm{P}\left(\log{5},~\frac{9\sqrt{5}}{5}\right)~~~~\cdots \fbox{答}\end{align}
geogebraによるシミュレーション
\(a\) の変化に応じて \(y=f(x)\) のグラフが移動していく様子を調べることができます.
スライダーを左右に動かしてみてください.
ぴったり \(y=g(x)\) のグラフと共有点をただ一つもつ瞬間の \(a\) の値が実際に \(2\sqrt{5}\fallingdotseq 4.47\) くらいになっていることが確認できます.





2015年第3問のコピー-120x68.jpg)

コメント