問題文全文
以下の問いに答えなさい.
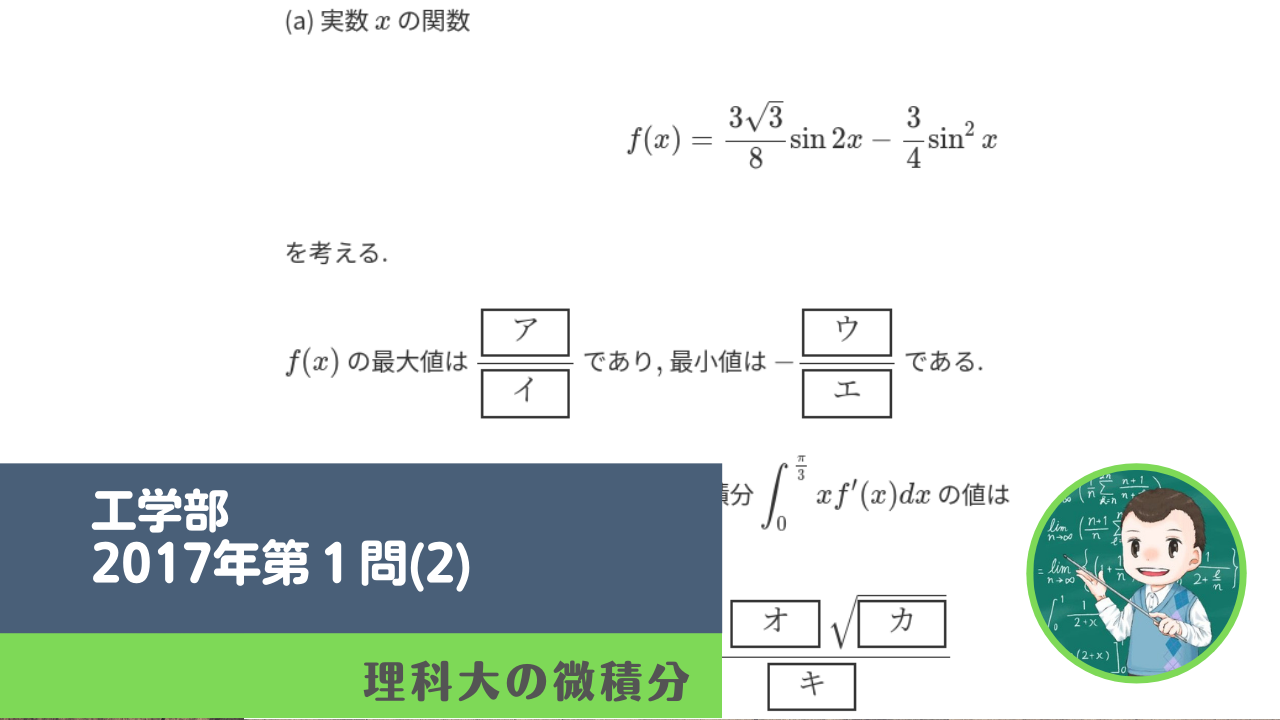
(a) 実数 \(x\) の関数
\begin{align}f(x)=\frac{3\sqrt{3}}{8}\sin{2x}-\frac{3}{4}\sin^2x\end{align}
を考える.
\(f(x)\) の最大値は \(\displaystyle \frac{\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) であり\(,\) 最小値は \(\displaystyle -\frac{\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) である.
\(f^{\prime}(x)\) を \(f(x)\) の導関数とするとき\(,\) 定積分 \(\displaystyle \int_0^{\frac{\pi}{3}}xf^{\prime}(x)dx\) の値は
\begin{align} \frac{\pi -\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~\sqrt{\fbox{$\hskip0.8emカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である.
(b) 実数 \(x\) の関数
\begin{align}g(x)=\frac{3\sqrt{3}}{8}a\sin{2x}-\frac{3}{4}a\sin^2{x}+\frac{3}{4}+b~~\left(0\leqq x \leqq \frac{\pi}{2}\right)\end{align}
を考える. ただし\(,\) \(a,~b\) は実数の定数で\(,\) \(a>0\) とする.
\(\displaystyle a=\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~,~b=-\frac{\fbox{$\hskip0.8emケコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) のとき\(,\) \(g(x)\) は
\begin{align} x=\frac{\pi}{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}} で最大値 \frac{3}{2}~,~x=\frac{\pi}{\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}} で最小値 -\frac{15}{2}\end{align}
をとる.
(a) の着眼点
三角関数の最大・最小問題で \(\sin^2{x}\) が出てきた場合\(,\) 以下の \(2\) つの変形が候補として上がります. 問題に応じて適切な方に変形をします. (\(\cos^2{x}\) も同様)
\begin{align}\begin{array}{ccc}① & \sin^2{x}=1-\cos^2{x} &(三角関数の相互関係)\\ ② & \displaystyle \sin^2{x}=\frac{1-\cos{2x}}{2} & (半角の公式)\end{array}\end{align}
今回は ② の変形をすることで\(,\) \(\sin{2x}\) と \(\cos{2x}\) の \(1\) 次式にできるため\(,\) 三角関数の合成から最大値・最小値を考えることができます.
もしくは今回の場合は後半の問題で \(xf^{\prime}(x)\) の積分を計算しなければならないのを見越して\(,\) 微分して増減表をかくことで最大・最小を求めるということも考えられます. その際\(,\) 定義域がすべての実数となっているので\(,\) 周期性に注目すると増減表のサイズを小さくできます.(別解で紹介します.)
(a) の前半の解答
\begin{align}f(x)=\frac{3\sqrt{3}}{8}\sin{2x}-\frac{3}{4}\sin^2{x}\end{align}
\begin{align}=\frac{3\sqrt{3}}{8}\sin{2x}-\frac{3}{8}(1-\cos{2x})\end{align}
\begin{align}=\frac{3\sqrt{3}}{8}\sin{2x}+\frac{3}{8}\cos{2x}-\frac{3}{8}\end{align}
\begin{align}=\frac{3}{4}\sin{\left(2x+\frac{\pi}{6}\right)}-\frac{3}{8}\end{align}
\(x\) はすべての実数であるから\(,\)
\begin{align}-1\leqq \sin{\left(2x+\frac{\pi}{6}\right)}\leqq 1\end{align}
\begin{align}-\frac{3}{4}\leqq \frac{3}{4}\sin{\left(2x+\frac{\pi}{6}\right)}\leqq \frac{3}{4}\end{align}
\begin{align}-\frac{9}{8}\leqq f(x) \leqq \frac{3}{8}\end{align}
\begin{align}最大値~\frac{3}{8}~,~最小値~-\frac{9}{8}~~~~\cdots \fbox{答}\end{align}
微分による別解
\begin{align}f(x)=\frac{3\sqrt{3}}{8}\sin{2x}-\frac{3}{4}\sin^2{x}\end{align}
\begin{align}f^{\prime}(x)=\frac{3\sqrt{3}}{4}\cos{2x}-\frac{3}{2}\sin{x}\cos{x}\end{align}
\begin{align}=\frac{3\sqrt{3}}{4}\cos{2x}-\frac{3}{4}\sin{2x}\end{align}
\begin{align}=\frac{3}{2}\cos{\left(2x+\frac{\pi}{6}\right)}\end{align}

quandle
\(\cos\) の合成で計算しています. 難しければ \(\sin \) で合成して \(\displaystyle \frac{\pi}{2}\) 回転することで \(\cos \) にできます.
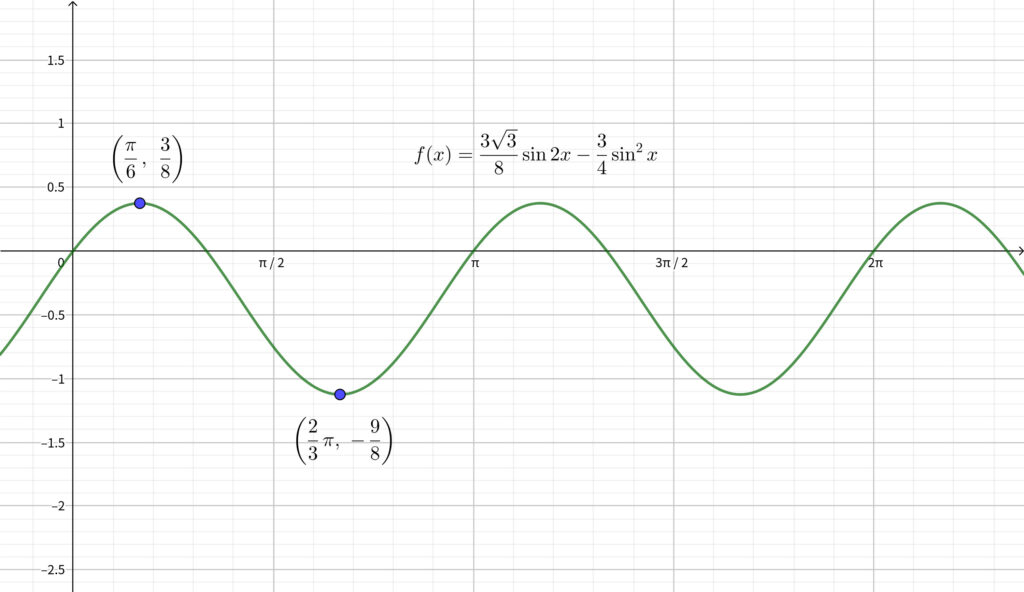
ここで\(,\) \(y=\sin{2x},~y=\sin{x}\) はどちらも周期 \(\pi\) であるから\(,\) \(y=f(x)\) も周期 \(\pi\) である. よって\(,\) 定義域を \(0\leqq x \leqq \pi\) としてよい. 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|}\hline x & 0 & \cdots & \displaystyle \frac{\pi}{6} & \cdots & \displaystyle \frac{2}{3}\pi & \cdots & \pi \\ \hline f^{\prime}(x) & {} & + & 0 & – & 0 & + & {} \\ \hline f(x) & 0 & \nearrow & \displaystyle \frac{3}{8} & \searrow & \displaystyle -\frac{9}{8} & \nearrow & 0 \\ \hline \end{array}\end{align}
増減表より\(,\)
\begin{align}最大値~\frac{3}{8}~,~最小値~-\frac{9}{8}~~~~\cdots \fbox{答}\end{align}
※なお \(y=f(x)\) のグラフは以下のようになります. 周期が \(\pi\) であることも確認できます.
(a) の後半の解答
\begin{align}f^{\prime}(x)=\frac{3}{2}\cos{\left(2x+\frac{\pi}{6}\right)}\end{align}
\begin{align}\int_0^{\frac{\pi}{3}}xf^{\prime}(x)dx=\frac{3}{2}\int_0^{\frac{\pi}{3}}x\cos{\left(2x+\frac{\pi}{6}\right)}dx\end{align}
\begin{align}=\frac{3}{2}\left\{\biggl[\frac{1}{2}x\sin{\left(2x+\frac{\pi}{6}\right)}\biggr]_0^{\frac{\pi}{3}}-\int_0^{\frac{\pi}{3}}\frac{1}{2}\sin{\left(2x+\frac{\pi}{6}\right)}dx\right\}\end{align}
\begin{align}=\frac{3}{4}\cdot \frac{\pi}{3}\cdot \frac{1}{2}+\frac{3}{8}\biggl[\cos{\left(2x+\frac{\pi}{6}\right)}\biggr]_0^{\frac{\pi}{3}}=\frac{\pi}{8}+\frac{3}{8}\left(-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\right)\end{align}
\begin{align}=\frac{\pi -3\sqrt{3}}{8}~~~~\cdots \fbox{答}\end{align}
ア:3 イ:8 ウ:9 エ:8 オ:3 カ:3 キ:8
(b) の着眼点
\(g(x)\) の式が明らかに \(f(x)\) を使って表せそうです. (a) の結果を使って計算を省略しましょう.
\(a,~b\) の2つの未知数がありますから\(,\) 最大値の条件から \(1\) つ\(,\) 最小値の条件から \(1\) つ式を立てれば解けそうです.
(b) の解答
\begin{align}g(x)=\frac{3\sqrt{3}}{8}a\sin{2x}-\frac{3}{4}a\sin^2{x}+\frac{3}{4}a+b\end{align}
\begin{align}=a\left(f(x)+\frac{3}{4}\right)+b=a\left\{\frac{3}{4}\sin{\left(2x+\frac{\pi}{6}\right)}+\frac{3}{8}\right\}+b\end{align}
\(\displaystyle 0\leqq x \leqq \frac{\pi}{2}\) より\(,\)
\begin{align}\frac{\pi}{6}\leqq 2x+\frac{\pi}{6} \leqq \frac{7}{6}\pi\end{align}
であるから\(,\)
\(\displaystyle 2x+\frac{\pi}{6}=\frac{\pi}{2}\) つまり\(,\) \(\displaystyle x=\frac{\pi}{6}\) のとき
\(\displaystyle \sin{\left(2x+\frac{\pi}{6}\right)}\) は最大値 \(1\) をとるので\(,\)
\begin{align}g(x)~の最大値は~\frac{9}{8}a+b~となる\end{align}
\(\displaystyle 2x+\frac{\pi}{6}=\frac{7}{6}\pi\) つまり\(,\) \(\displaystyle x=\frac{\pi}{2}\) のとき
\(\displaystyle \sin{\left(2x+\frac{\pi}{6}\right)}\) は最小値 \(\displaystyle -\frac{1}{2}\) をとるので\(,\)
\begin{align}g(x)~の最小値は~b~となる.\end{align}
条件より\(,\)
\begin{align}\left\{\begin{array}{c}\displaystyle \frac{9}{8}a+b=\frac{3}{2}\\ \displaystyle b=-\frac{15}{2}\end{array}\right.\end{align}
これを解いて\(,\)
\begin{align}a=8,~b=-\frac{15}{2}\end{align}
以上より\(,\) \(\displaystyle a=8,~b=-\frac{15}{2}\) のとき\(,\) \(g(x)\) は
\begin{align}x=\frac{\pi}{6}~で最大値~\frac{3}{2},~x=\frac{\pi}{2}~で最小値~-\frac{15}{2}~をとる~~~~\cdots \fbox{答}\end{align}
ク:8 ケ:1 コ:5 サ:2 シ:6 ス:2





コメント