東京理科大学理学部数学科専用2021年第１問| 理科大の微積分

理学部（数学科専用）2021年第１問の問題文全文
点 \(\mathrm{P}\) はどう動くか
速度と位置の関係
(1) の着眼点
(1) の解答
(2) の着眼点
(2) の解答
(3) の着眼点
(3) の解答
(4) の解答

理学部（数学科専用）2021年第１問の問題文全文

\(c\) を正の定数とし\(,\) \(0<T_1<T_2<T_3<1\) とする. 座標平面上を次のように運動する点 \(\mathrm{P}\) について考える. ただし\(,\) 時刻 \(t\) における点 \(\mathrm{P}\) の座標を \((f(t),~g(t))\) とするとき\(,\) \(f(t)\) と \(g(t)\) は \(0\leqq t \leqq 1\) において連続であるとする.

●　\((f(0),~g(0))=(0,~0)\) である. \(0<t<T_1\) のとき\(,\) 時刻 \(t\) における点 \(\mathrm{P}\) の速度は \((c,~0)\) である. \(a=f(T_1)\) とおく.

●　\((f(T_1),~g(T_1))=(a,~0)\) である. \(T_1<t<T_2\) のとき\(,\) 時刻 \(t\) における点 \(\mathrm{P}\) の速度は \(\displaystyle \left(0,~\frac{a}{t}\right)\) である. \(b=g(T_2)\) とおく.

●　\((f(T_2),~g(T_2))=(a,~b)\) である. \(T_2<t<T_3\) のとき\(,\) 時刻 \(t\) における点 \(\mathrm{P}\) の速度は \(\displaystyle \left(-\frac{a}{t},~0\right)\) である.

●　\((f(T_3),~g(T_3))=(0,~b)\) である. \(T_3<t<1\) のとき\(,\) 時刻 \(t\) における点 \(\mathrm{P}\) の速度は \(\displaystyle \left(0,-\frac{a}{t}\right)\) である.

(1) \(c,~T_1\) を用いて\(,\) \(a\) を表せ.

(2) \(a,~T_1,~T_2\) を用いて\(,\) \(b\) を表せ.

(3) \((f(1),~g(1))=(0,~0)\) であるとき\(,\) \(T_1\) を用いて\(,\) \(T_2,~T_3\) を表せ. また\(,\) \(c,~T_1\) を用いて\(,\) \(a\) と \(b\) の積 \(ab\) を表せ.

(4) (3) で求めた \(ab\) を変数 \(T_1\) の関数と考える. \(T_1\) が \(\displaystyle 0<T_1 <\frac{1}{e}\) の範囲を動くとき\(,\) \(ab\) の最大値を求めよ. ただし\(,\) \(e\) は自然対数の底を表す.

点 \(\mathrm{P}\) はどう動くか

問題文が長く状況を理解するのに時間がかかると思います. こういう問題はしっかり状況を理解することが何より大事なので時間をかけましょう.

点 \(\mathrm{P}\) の動きはわかりますか？結論だけ先にかいておくと以下のように動きます.

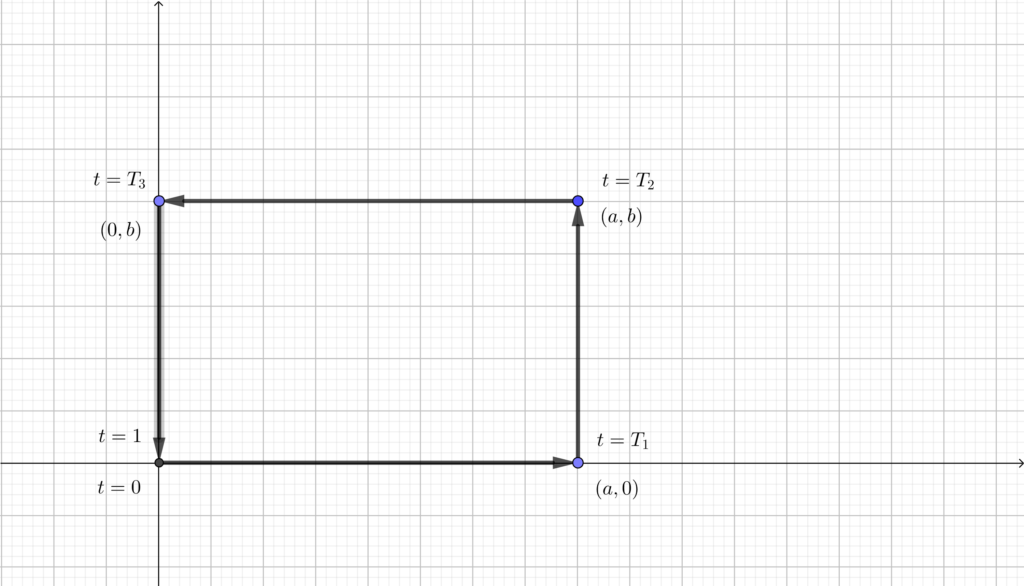
原点からスタートして\(,\) \((a,~0)~\rightarrow ~(a,~b)~\rightarrow ~(0,~b)~\rightarrow ~(0,~0)\) の順に反時計回りに動きます.

速度と位置の関係

時間 \(t\) に関する位置 \(x(t)\)\(,\) 速度 \(v(t)\) が与えられているとき\(,\) 以下の関係が成り立ちます.

\(t=t_1\) から \(t=t_2\) における位置の変化（変位）は

\begin{align}\int_{t_1}^{t_2}v(t)dt\end{align}

で与えられる.

(1) の着眼点

\((f(0),~g(0))=(0,~0)\)とあるので\(,\) 最初点 \(\mathrm{P}\) は原点にあることがわかります.

速度は \((c,~0)\) です. \(c\) は定数なので\(,\) \(x\) 軸方向には等速で運動をするということです.

\(y\) 成分は常に \(0\) なので\(,\) \(y\) 軸方向へは一切移動しないということです.

つまり\(,\) \(0<t<T_1\) のとき\(,\) 点 \(\mathrm{P}\) は原点を出発して \(x\) 軸方向へ等速 \(c\) で移動し\(,\) \(t=T_1\) のときに\(,\) \((a,~0)\) にたどり着くということです.

(1) の解答

\begin{align}a=cT_1~~~~\cdots \fbox{答}\end{align}

quandle

公式どおりに

\begin{align}\int_0^{T_1}cdt\end{align}

としてももちろん求められます. 今回は等速運動なので

（速さ）×（時間）

で出しました. （「みはじ」とかやりましたね）

(2) の着眼点

今度は速度が \(\displaystyle \left(0,~\frac{a}{t}\right)\) ですから\(,\) \(y\) 軸方向にのみ移動することになります. 今回は速度ベクトルの\(y\) 成分が定数でなく\(,\) \(t\) の関数ですから\(,\) 積分して変位を求めることになります.

(2) の解答

\begin{align}b=\int_{T_1}^{T_2}\frac{a}{t}dt\end{align}

\begin{align}=\biggl[a\log{t}\biggr]_{T_1}^{T_2}=a\log{\frac{T_2}{T_1}}~~~~\cdots \fbox{答}\end{align}

(3) の着眼点

考え方は (1) \(,\) (2) と同じですが\(,\) \(T_2<t<T_3\) においては \(x\) 軸方向と逆に進むので変位は \(-a\) とすること\(,\) \(T_3<t<1\) においては \(y\) 軸方向と逆に進むので変位は \(-b\) とすることに注意して計算をしましょう.

(3) の解答

\begin{align}-a=\int_{T_2}^{T_3}-\frac{a}{t}dt\end{align}

\begin{align}a=\biggl[a\log{t}\biggr]_{T_2}^{T_3}\end{align}

\begin{align}\log{\frac{T_3}{T_2}}=1\end{align}

\begin{align}T_3=eT_2~~~~\cdots ①\end{align}

\begin{align}-b=\int_{T_3}^1-\frac{a}{t}dt\end{align}

\begin{align}b=\biggl[a\log{t}\biggr]_{T_3}^1=-a\log{T_3}~~~~\cdots ②\end{align}

(2)\(,\) ①\(,\) ②より

\begin{align}\log{\frac{T_2}{T_1}}=-\log{T_3}\end{align}

\begin{align}\frac{T_2}{T_1}=\frac{1}{T_3}\end{align}

\begin{align}T_2=\frac{T_1}{T_3}=\frac{T_1}{eT_2}\end{align}

\begin{align}eT_2^2=T_1\end{align}

\(T_2>0\) より\(,\)

\begin{align}T_2=\sqrt{\frac{T_1}{e}}~~~~\cdots \fbox{答}\end{align}

\begin{align}T_3=e\sqrt{\frac{T_1}{e}}=\sqrt{eT_1}~~~~\cdots \fbox{答}\end{align}

\begin{align}ab=-a^2\log{T_3}\end{align}

\begin{align}=-c^2T_1^2\log{\sqrt{eT_1}}=-c^2T_1^2\cdot \frac{1}{2}(1+\log{T_1})\end{align}

\begin{align}=-\frac{c^2}{2}T_1^2(1+\log{T_1})~~~~\cdots \fbox{答}\end{align}

(4) の解答

\begin{align}F(T_1)=T_1^2(1+\log{T_1})\end{align}

とおく. \(\displaystyle -\frac{c^2}{2}<0\) より\(,\) \(ab\) が最大であることと\(,\) \(F(T_1)\) が最小であることは必要十分である.

\begin{align}F^{\prime}(T_1)=2T_1(1+\log{T_1})+T_1^2\cdot \frac{1}{T_1}=T_1(3+2\log{T_1})\end{align}

\(T_1>0\) より\(,\) \(3+2\log{T_1}\) の符号と \(F^{\prime}(T_1)\) の符号は一致する. よって\(,\) 増減表は以下のようになる.

\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline T_1 & 0 & \cdots & e^{-\frac{3}{2}} & \cdots & e^{-1} \\ \hline F^{\prime}(T_1) & {} & – & 0 & + & {}\\ \hline F(T_1) & {} & \searrow & 極小 & \nearrow & {} \\ \hline \end{array}\end{align}

増減表より\(,\) \(F(T_1)\) の最小値は

\begin{align}F\left(e^{-\frac{3}{2}}\right)=e^{-3}\left(1-\frac{3}{2}\right)=-\frac{1}{2e^3}\end{align}

よって\(,\) \(ab\) の最大値は

\begin{align}-\frac{c^2}{2}\left(-\frac{1}{2e^3}\right)=\frac{c^2}{4e^3}~~~~\cdots \fbox{答}\end{align}