公立諏訪東京理科大学 推薦 第４問の問題文全文
関数 \(f(x)=|x^2+2x-3|-|x+3|\) について\(,\) 以下の問いに答えよ.
(1) 方程式 \(f(x)=0\) となる \(x\) の値を求めよ.
(2) \(-3\leqq x \leqq 2\) において\(,\) \(f(x)\) の最大値と最小値を求めよ.
(3) 座標平面において放物線 \(y=x^2+2x-3\) と直線 \(y=x+3\) の交点の \(x\) 座標をそれぞれ\(,\) \(\alpha\) \(,\) \(\beta\) ( ただし\(,\) \(\alpha <\beta \) ) とする. このとき\(,\) 定積分 \(\displaystyle \int_{\alpha}^{\beta}f(x)dx\) の値を求めよ.
(1) の着眼点〜絶対値の処理〜
絶対値が \(2\) つついているのでそれぞれが正のときと負のときで合計 \(4\) パターンの場合分けが必要と考えるかもしれませんが\(,\) 今回はそれを避けることができます.
\begin{align}|a|=|b|~\Leftrightarrow a=\pm b\end{align}
上記の形であれば場合分けをせず一気に処理できるのでぜひ活用しましょう.
(1) の解答〜|a|=|b|の形に帰着させる〜
\begin{align}|x^2+2x-3|=|x+3|\end{align}
\begin{align}x^2+2x-3=\pm(x+3)\end{align}
\begin{align}x^2+x-6=0~\mathrm{or}~x^2+3x=0\end{align}
\begin{align}(x+3)(x-2)=0~\mathrm{or}~x(x+3)=0\end{align}
\begin{align}x=-3,~0,~2~~~~\cdots \fbox{答}\end{align}
(2) の解答〜符号の処理を正確に〜
\(-3 \leqq x \leqq 2\) のとき\(,\) \(x+3 \geqq 0\) であるから\(,\)
\begin{align}|x+3| \geqq 0\end{align}
\(x^2+2x-3=(x+3)(x-1)\) であるから\(,\)
\begin{align}|x^2+2x-3|=\left\{\begin{array}{cc}-(x^2+2x-3) & (-3\leqq x \leqq 1) \\ x^2+2x-3 & (1\leqq x \leqq 2) \end{array}\right.\end{align}
よって\(,\) \(f(x)\) は以下のようになる.
\begin{align}f(x)=\left\{\begin{array}{cc}-(x^2+2x-3)-(x+3) & (-3\leqq x \leqq 1) \\ x^2+2x-3-(x+3) & (1\leqq x \leqq 2)\end{array}\right.\end{align}
\begin{align}=\left\{\begin{array}{cc}-x^2-3x & (-3\leqq x \leqq 1) \\ x^2+2x-6 & (1\leqq x \leqq 2)\end{array}\right.\end{align}
\begin{align}=\left\{\begin{array}{cc}\displaystyle -\left(x+\frac{3}{2}\right)^2+\frac{9}{4} & (-3 \leqq x \leqq 1) \\ \displaystyle \left(x+\frac{1}{2}\right)^2-\frac{25}{4} & (1\leqq x \leqq 2)\end{array}\right.\end{align}
\(f(x)\) のグラフは以下のようになる.
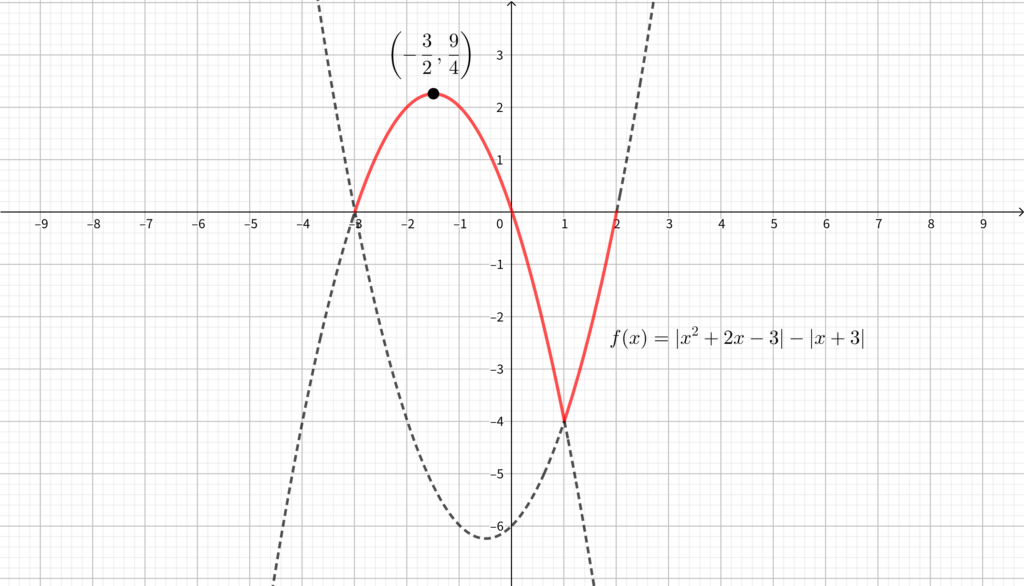
グラフより\(,\)
\begin{align}x=-\frac{3}{2}~のとき,~最大値~\frac{9}{4}~~~~\cdots \fbox{答}\end{align}
\begin{align}x=1~のとき,~最小値~-4~~~~\cdots \fbox{答}\end{align}
(3) の解答〜必要なものはすでに揃っているので計算あるのみ〜
(1) より\(,\)
\begin{align}\alpha =-3,~\beta =2\end{align}
よって\(,\) 求める定積分は\(,\)
\begin{align}\int_{-3}^2f(x)dx=\int_{-3}^1(-x^2-3x)dx+\int_1^2(x^2+x-6)dx\end{align}
\begin{align}=\biggl[-\frac{1}{3}x^3-\frac{3}{2}x^2\biggr]_{-3}^1+\biggl[\frac{1}{3}x^3+\frac{1}{2}x^2-6x\biggr]_1^2\end{align}
\begin{align}=-\frac{1}{3}\{1-(-27)\}-\frac{3}{2}(1-9)+\frac{1}{3}(8-1)+\frac{1}{2}(4-1)-6(2-1)\end{align}
\begin{align}=-\frac{28}{3}+12+\frac{7}{3}+\frac{3}{2}-6=\frac{1}{2}~~~~\cdots \fbox{答}\end{align}
コメント