問題文全文
以下の問いに答えなさい. ただし, 空欄 \(\fbox{$\hskip0.8em(あ)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) 〜 \(\fbox{$\hskip0.8em(き)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) については適切な数または式を解答用紙の所定の欄に記入しなさい.
(1) 実数 \(x\) の関数
\begin{align}f(x)=\frac{3x+\sqrt{32-7x^2}}{4}\end{align}
の定義域は \(\fbox{$\hskip0.8em(あ)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\leqq x \leqq \fbox{$\hskip0.8em(い)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である. また, \(f(x)\) は, \(x=\fbox{$\hskip0.8em(う)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) のとき \(f(x)=0\) となり, \(x=\fbox{$\hskip0.8em(え)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) のとき極大値 \(\fbox{$\hskip0.8em(お)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) をとる.
(2) 座標平面上の曲線
\begin{align}2x^2-3xy+2y^2=4\end{align}
について以下の問いに答えなさい.
(a) 曲線で囲まれた部分の面積は \(\fbox{$\hskip0.8em(か)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である.
(b) 曲線で囲まれた部分を \(x\) 軸の周りに 1 回転させてできる立体の体積は \(\fbox{$\hskip0.8em(き)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である. なお, (き)を導く過程を所定の場所に書きなさい.
(1) の解答
\(f(x)\) の定義域は
\begin{align}32-7x^2\geqq 0\Leftrightarrow (\sqrt{7}x+4\sqrt{2})(\sqrt{7}x-4\sqrt{2})\leqq 0\end{align}
\begin{align}\Leftrightarrow -\frac{4\sqrt{2}}{7}\leqq x\leqq \frac{4\sqrt{2}}{\sqrt{7}}\Leftrightarrow -\frac{4\sqrt{14}}{7}\leqq x\leqq \frac{4\sqrt{14}}{7}.\end{align}
また, \(f(x)=0\) となるのは,
\begin{align}3x+\sqrt{32-7x^2}=0\Leftrightarrow \sqrt{32-7x^2}=-3x\end{align}
のときである. この等式が成り立つのは \(x\leqq 0\) のときで, 両辺を 2 乗すると
\begin{align}32-7x^2=9x^2\Leftrightarrow x^2=2\end{align}
\(x\leqq 0\) より,
\begin{align}x=-\sqrt{2}\end{align}
となる.
\(\displaystyle -\frac{4\sqrt{14}}{7}<x<\frac{4\sqrt{14}}{7}\) において,
\begin{align}f^{\prime}(x)=\frac{1}{4}\left(3+\frac{-14x}{2\sqrt{32-7x^2}}\right)=\frac{3\sqrt{32-7x^2}-7x}{4\sqrt{32-7x^2}}\end{align}

quandle
無理関数はルートの中身が 0 になるような \(x\) では微分不可です.
だから, \(f^{\prime}(x)\) の定義域には等号がついていません.
\(f^{\prime}(x)=0\) のとき
\begin{align}3\sqrt{32-7x^2}-7x=0\Leftrightarrow 3\sqrt{32-7x^2}=7x\end{align}
この等式が成り立つのは \(x\geqq 0\) のときで, 両辺を 2 乗すると
\begin{align}9(32-7x^2)=49x^2\Leftrightarrow 112x^2=288\Leftrightarrow x^2=\frac{18}{7}\end{align}
\(x\geqq 0\) より
\begin{align}x=\frac{3\sqrt{2}}{\sqrt{7}}=\frac{3\sqrt{14}}{7}\end{align}
よって, 増減表は以下のようになる.
\begin{array}{c|c|c|c|c|c|}x & \displaystyle -\frac{4\sqrt{14}}{7} & \cdots & \displaystyle \frac{3\sqrt{14}}{7} & \cdots & \displaystyle \frac{4\sqrt{14}}{7} \\ \hline f^{\prime}(x) & \times & + & 0 & – & \times \\ \hline f(x) & \displaystyle -\frac{3\sqrt{14}}{7} & \nearrow & 極大 & \searrow & \displaystyle \frac{3\sqrt{14}}{7} \\ \end{array}
増減表より, \(\displaystyle \frac{3\sqrt{14}}{7}\) のとき極大値
\begin{align}f\left(\frac{3\sqrt{14}}{7}\right)=\frac{1}{4}\left(\frac{9\sqrt{14}}{7}+\sqrt{14}\right)=\frac{1}{4}\cdot \frac{16\sqrt{14}}{7}=\frac{4\sqrt{14}}{7}.\end{align}
(2) の (a) の着眼点
①
\begin{align}Ax^2+2Bxy+Cy^2=1~~(A>0,~C>0,~AC-B^2>0)\end{align}
の形は「斜めの楕円」になるという事実を知っている人はだいぶ見通しよく解けると思います.
ですが, 普通の受験生は上記事実を知らないと思います. 知らなくてももちろん解けます.
② (1) と何か関係がないでしょうか. (1) の \(f(x)\) の形をよくみると, なんだか解の公式に見えてきます. そこで \(y\) の 2 次方程式だと思って解の公式を使ってみましょう. 見事に (1) の形が出てきます.
③ (2) の式は (1) の \(f(x)\) と ルートの前の符号が逆になった関数 \(\displaystyle g(x)=\frac{3x-\sqrt{32-7x^2}}{4}\) の貼り合わせになっています.
\(g(-x)=-f(x)\) が成り立つので, \(g(x)\) のグラフは, \(f(x)\) のグラフを原点に関して対称移動したものです. そして \(f(x)\) のグラフは (1) の増減表を利用してかくことができます.
(2) の (a) の解答
\begin{align}2x^2-3xy+2y^2=4\Leftrightarrow 2y^2-3xy+2x^2-4=0\end{align}
を \(y\) について解くと
\begin{align}y=\frac{3x\pm \sqrt{32-7x^2}}{4}\end{align}
となる.
\begin{align}f(x)=\frac{3x+\sqrt{32-7x^2}}{4},~~g(x)=\frac{3x-\sqrt{32-7x^2}}{4}\end{align}
とおくと, \(g(-x)=-f(x)\) より, \(y=g(x)\) のグラフは \(y=f(x)\) のグラフを原点に関して対称移動させたものになる.
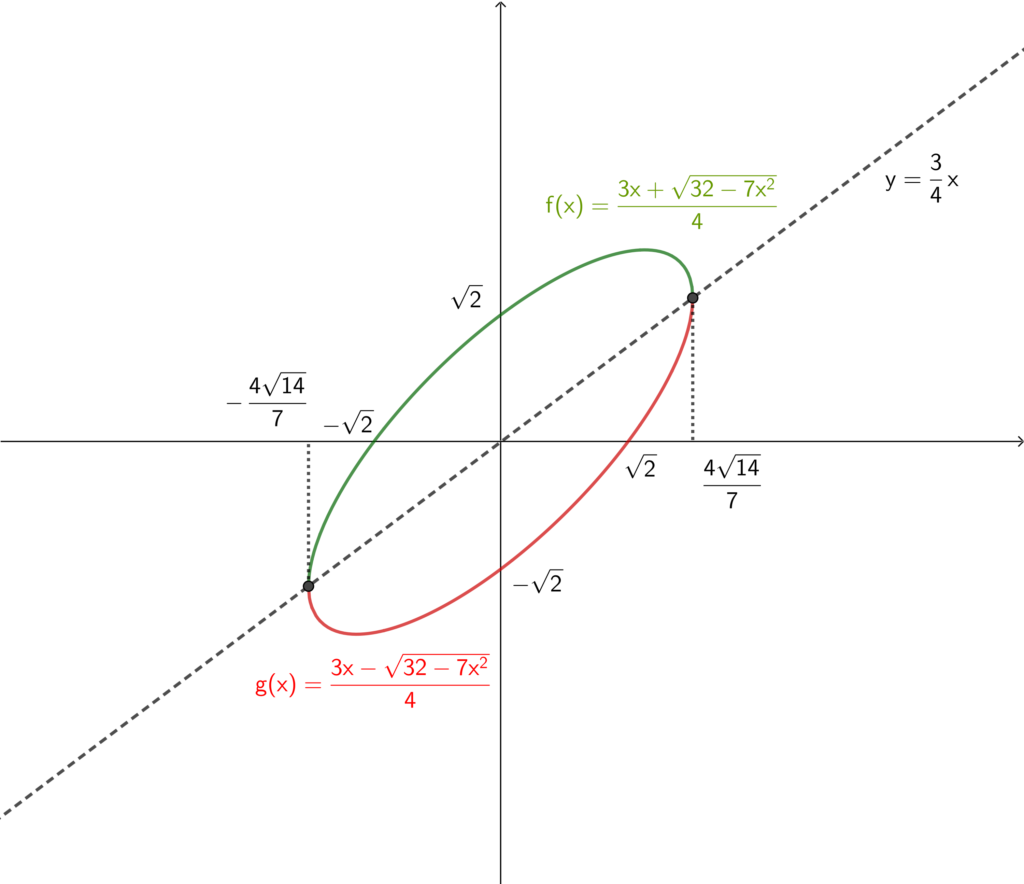
(1) の増減表と合わせると,
\begin{align}2x^2-3xy+2y^2=4\end{align}
は以下の図のようになる.
求める面積を \(S\) とおくと
\begin{align}S=\int_{-\frac{4\sqrt{14}}{7}}^{\frac{4\sqrt{14}}{7}}\{f(x)-g(x)\}dx=\int_{-\frac{4\sqrt{14}}{7}}^{\frac{4\sqrt{14}}{7}}\frac{\sqrt{32-7x^2}}{2}dx\end{align}
\begin{align}=\int_0^{\frac{4\sqrt{14}}{7}}\sqrt{32-7x^2}dx=\frac{1}{4}\cdot 4\sqrt{2}\cdot \frac{4\sqrt{14}}{7}\pi=\frac{8\sqrt{7}}{7}\pi.\end{align}

quandle
\begin{align}\int_0^{\frac{4\sqrt{14}}{7}}\sqrt{32-7x^2}dx\end{align}
の計算は置換積分でもできますが, 楕円の面積を利用しましょう.
\begin{align}y=\sqrt{32-7x^2}\end{align}
とおくと,
\begin{align}y^2=32-7x^2\Leftrightarrow \cfrac{x^2}{\cfrac{32}{7}}+\frac{y^2}{32}=1\end{align}
なので, 長軸半径 \(4\sqrt{2}\), 短軸半径 \(\displaystyle \frac{4\sqrt{14}}{7}\) の楕円の \(\displaystyle \frac{1}{4}\) 個分の面積になります.
(2) の (a) の別解(行列式の利用)
※現行過程(2020年現在)では行列は範囲外ですのであくまでも参考程度に読んでください.
\begin{align}2x^2-3xy+2y^2=4\Leftrightarrow 2\left(x-\frac{3}{4}y\right)^2+\frac{7}{8}y^2=4\end{align}
\begin{align}\Leftrightarrow \cfrac{\left(x-\cfrac{3}{4}y\right)^2}{2}+\cfrac{y^2}{\cfrac{32}{7}}=1\end{align}
より, \(\displaystyle X=x-\frac{3}{4}y,~Y=y\) とおくと,
\begin{align}\frac{X^2}{2}+\cfrac{Y^2}{\cfrac{32}{7}}=1\end{align}
であり, これは \(XY\) 平面における楕円を表す. この楕円は長軸半径 \(\displaystyle \frac{4\sqrt{14}}{7}\), 短軸半径 \(\sqrt{2}\) である.
\begin{align}\begin{pmatrix}X \\ Y\end{pmatrix}=\begin{pmatrix}1 & \displaystyle -\frac{3}{4} \\ 0 & 1\end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix}\end{align}
が成り立つから, 曲線 \(2x^2-3xy+2y^2=4\) は 1 次変換
\begin{align}A=\begin{pmatrix}1 & \displaystyle -\frac{3}{4} \\ 0 & 1\end{pmatrix}\end{align}
により, 楕円 \(\displaystyle \frac{X^2}{2}+\cfrac{Y^2}{\cfrac{32}{7}}=1\) に変換される.
\begin{align}detA=1\cdot 1-\left(-\frac{3}{4}\right)\cdot 0=1\end{align}
より変換倍率は 1 である. よって求める面積は
\begin{align}\frac{4\sqrt{14}}{7}\cdot \sqrt{2}\cdot 1\cdot \pi=\frac{8\sqrt{7}}{7}\pi.\end{align}

quandle
直交座標平面における曲線は 1 次変換 \(A\) によって, 斜交座標平面に移されます. その際, 面積は \(detA\) 倍になります.
(2) の (b) の着眼点
① \(x\) 軸回転の問題です. (a) のときにかいた曲線をみると \(x\) 軸より下の部分にも曲線があります. この場合は \(x\) 軸より下の部分を \(x\) 軸に関して対称に折り返した部分を回転させることになります. 下図のピンク色の部分です.

② 上図から分かるように出来上がる回転体は \(y\) 軸に関して対称になります. \(y\) 軸より右側の体積を求め, それを 2 倍しましょう.
③ \(0\leqq x\leqq \sqrt{2}\) については上図の緑の関数を積分するだけですが, \(\displaystyle \sqrt{2}\leqq x\leqq \frac{4\sqrt{14}}{7}\) については緑の関数から赤の関数を引いたものを積分する必要があります.
(2) の (b) の解答
曲線 \(2x^2-3xy+2y^2=4\) を \(x\) 軸に関して回転させてできる立体は上図のピンク色の部分を \(x\) 軸に関して回転させてできる立体となる.
これは \(y\) 軸に関して対称であるから, \(x\geqq 0\) 部分の体積を 2 倍すればよい.
求める体積を \(V\) とおくと,
\begin{align}\frac{V}{2}=\pi \int_0^{\sqrt{2}}\left(\frac{3x+\sqrt{32-7x^2}}{4}\right)^2dx+\pi \int_{\sqrt{2}}^{\frac{4\sqrt{14}}{7}}\left\{\left(\frac{3x+\sqrt{32-7x^2}}{4}\right)^2-\left(\frac{3x-\sqrt{32-7x^2}}{4}\right)^2\right\}dx\end{align}
\begin{align}=\pi \int_0^{\sqrt{2}}\left(\frac{1}{8}x^2+\frac{3}{8}x\sqrt{32-7x^2}+2\right)dx+\pi \int_{\sqrt{2}}^{\frac{4\sqrt{14}}{7}}\frac{3}{4}x\sqrt{32-7x^2}dx\end{align}
\begin{align}=\pi \int_0^{\sqrt{2}}\left\{\frac{1}{8}x^2+\frac{3}{8}\left(-\frac{1}{14}\right)(32-7x^2)^{\prime}\sqrt{32-7x^2}+2\right\}dx+\pi \int_{\sqrt{2}}^{\frac{4\sqrt{14}}{7}}\frac{3}{4}\left(-\frac{1}{14}\right)(32-7x^2)^{\prime}\sqrt{32-7x^2}dx\end{align}
\begin{align}=\pi \biggl[\frac{1}{24}x^3-\frac{3}{112}\cdot \frac{2}{3}(32-7x^2)^{\frac{3}{2}}+2x\biggr]_0^{\sqrt{2}}+\pi \biggr[-\frac{3}{56}\cdot \frac{2}{3}(32-7x^2)^{\frac{3}{2}}\biggr]_{\sqrt{2}}^{\frac{4\sqrt{14}}{7}}\end{align}
\begin{align}=\pi \left\{\left(\frac{\sqrt{2}}{12}-\frac{27\sqrt{2}}{28}+2\sqrt{2}\right)+\frac{16\sqrt{2}}{7}\right\}+\frac{27\sqrt{2}}{14}\pi=\frac{(7-81+168+192+162)\sqrt{2}}{84}\pi\end{align}
\begin{align}=\frac{448\sqrt{2}}{84}\pi=\frac{16\sqrt{2}}{3}\pi.\end{align}
よって,
\begin{align}V=\frac{32\sqrt{2}}{3}\pi.\end{align}







2020年第3問3-120x68.jpg)

コメント