理学部（応数・応物・応化）2022年第１問(1)

理（応数・応物・応化）

2023.01.02

東京理科大学理学部（応数・応物・応化）2022年第１問(1)の問題文全文
(a) の解答〜線分 $\mathrm{AB}$ が $yz$ 平面と垂直であることに気付けるか〜
1. $S$ の形を把握する〜動いているものが複数あるときは１つずつ動かす〜
  1. $\mathrm{P}$ を固定して $\mathrm{Q}$ だけ動かす
  2. 点 $\mathrm{P}$ を動かして $\triangle \mathrm{PDC}$ の通過領域を考える
(b) の解答〜 $S$ を $z=t$ で切って回転させる〜

東京理科大学理学部（応数・応物・応化）2022年第１問(1)の問題文全文

座標空間内に $4$ 点 $\mathrm{A}(1,~0,~1)$$,$ $\mathrm{B}(-1,~0,~1)$$,$ $\mathrm{C}(0,~1,~-1)$$,$ $\mathrm{D}(0,~-1,~-1)$ をとる. 点 $\mathrm{P}$ が線分 $\mathrm{AB}$ 上を動き$,$ 点 $\mathrm{Q}$ が線分 $\mathrm{CD}$ 上を動くとき$,$ 線分 $\mathrm{PQ}$ 上の点が通過し得る領域を $S$ とする. このとき以下が成り立つ.

(a) $S$ の体積は $\displaystyle \frac{~\fbox{$\hskip0.4emア\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emイ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}$ である.

(b) $z$ 軸の周りに $S$ を $1$ 回転させてできる立体の体積は $\displaystyle \frac{~\fbox{$\hskip0.4emウ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emエ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\pi$ である.

(a) の解答〜線分 $\mathrm{AB}$ が $yz$ 平面と垂直であることに気付けるか〜

立体 $S$ は四面体 $\mathrm{ABCD}$ となる. （理由は後述します）

$\mathrm{A}(1,~0,~1),~\mathrm{B}(-1,~0,~1)$ は $y$ 座標と $z$ 座標が一致しているので$,$ 線分 $\mathrm{AB}$ と $yz$ 平面は垂直である. （今回は特に $x$ 座標が異符号なので$,$ $yz$ 平面と対称な点であることもわかります.）

quandle

ピンと来ない人はベクトルで考えるとわかりやすいです. $\overrightarrow{\mathrm{AB}}=(-2,~0,~0)$ で$,$ $yz$ 平面上の任意のベクトルは $(0,~y,~z)$ とかけるので$,$

\begin{align}(-2,~0,~0)\cdot (0,~y,~z)=0\end{align}

となり確かに $\overrightarrow{\mathrm{AB}}\perp yz 平面$ となっていることが分かりますね.

線分 $\mathrm{AB}$ 上の点で$,$ $yz$ 平面上にもある点を $\mathrm{M}$ とおくと$,$ $\mathrm{M}(0,~0,~1)$ であるから$,$ 三角形 $\mathrm{MCD}$ は $yz$ 平面上にあり$,$ 特に $\mathrm{MC}=\mathrm{MD}$ の二等辺三角形である. 線分 $\mathrm{CD}$ の中点を $\mathrm{N}(0,~0,~-1)$ とおく.

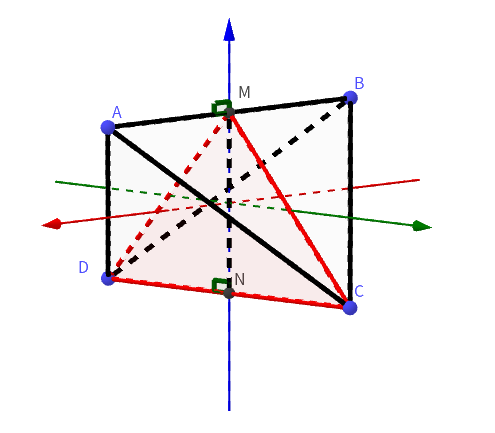
\begin{align}\triangle \mathrm{MCD}=\frac{1}{2}\cdot \mathrm{CD}\cdot \mathrm{MN}=\frac{1}{2}\cdot 2\cdot 2=2\end{align}

以上より$,$ $S$ の体積を $V$ とおくと$,$

\begin{align}V=\frac{1}{3}\cdot \triangle \mathrm{MCD}\cdot \mathrm{AB}=\frac{1}{3}\cdot 2\cdot 2=\frac{4}{3}~~~~\cdots \fbox{答}\end{align}

ア：４　イ：３

$S$ の形を把握する〜動いているものが複数あるときは１つずつ動かす〜

$\mathrm{P}$ を固定して $\mathrm{Q}$ だけ動かす

点 $\mathrm{P}$ と点 $\mathrm{Q}$ が同時に動いています. こういうときは $1$ つ固定すると考えやすくなります. 点 $\mathrm{P}$ を固定して点 $\mathrm{Q}$ だけを動かすと $\triangle \mathrm{PDC}$ ができます. 下図のようなイメージになります.

点 $\mathrm{P}$ を動かして $\triangle \mathrm{PDC}$ の通過領域を考える

次に点 $\mathrm{p}$ を動かして $\triangle \mathrm{PDC}$ の通過領域を考えることで $S$ がどんな形になるかを考えることができます. できあがった $S$ は四面体 $\mathrm{ABCD}$ となります. 下図のようなイメージになります.

(b) の解答〜 $S$ を $z=t$ で切って回転させる〜

$S$ を $z=t$ で切る〜各線分を内分した点を結ぶ〜

$S$ を $z=t$ で切ったときにできる切断面の図形は$,$ 線分 $\mathrm{AC}$$,$ 線分 $\mathrm{AD}$$,$ 線分 $\mathrm{BC}$$,$ 線分 $\mathrm{BD}$ をそれぞれ $(1-t)~:~(1+t)$ に内分した点を結んでできる図形で長方形である. この長方形を$T_t$ とおく.