問題文全文
座標平面上で\(,\) 直線 \(\ell ~:~x=-1\) 上の点 \(\mathrm{M}\) に対して\(,\) 原点 \(\mathrm{O}\) と \(\mathrm{M}\) を結ぶ直線上の点 \(\mathrm{P}\) を線分 \(\mathrm{MP}\) の長さが \(2\) で\(,\) \(\mathrm{P}\) と \(\mathrm{O}\) が \(\ell \) に関して同じ側にあるようにとる. \(\mathrm{M}\) が \(\ell \) 上を動くとき\(,\) \(\mathrm{P}\) が描く曲線を \(C\) とおく. 以下の問いに答えよ.
(1) \(\mathrm{M}\) の座標を \(\displaystyle (-1,~\tan{t})~~\left(-\frac{\pi}{2}<t<\frac{\pi}{2}\right)\) とするとき\(,\) \(\mathrm{P}\) の座標を \(t\) を用いて表せ.
(2) \(\displaystyle t=t_1 ,~t_2~~\left(-\frac{\pi}{2}<t_1 <t_2 <\frac{\pi}{2}\right)\) のとき\(,\) (1) で求めた \(\mathrm{P}\) の座標が一致するような \(t_1 ,~t_2\) を求めよ.
(3) \(C\) 上の点で\(,\) その点における \(C\) の接線が \(x\) 軸と垂直であるような点の座標を求めよ.
(4) \(C\) 上の点で\(,\) その点における \(C\) の接線が \(x\) 軸と平行であるような点が \(2\) つある. その点の \(x\) 座標を求めよ. また\(,\) \(2\) 点の \(y\) 座標の和も求めよ.
(5) \(\mathrm{M}\) が (2) で求めた \(t_1 ,~t_2\) に対して\(,\) \(t\) が \(t_1 \leqq t \leqq t_2\) の範囲を動くとき \(\mathrm{P}\) が描く曲線の概形を描け.
(6) (1) で求めた \(\mathrm{P}\) の座標を \((x(t),~y(t))\) とするとき\(,\) \(\displaystyle \int_{t_1}^{t_2} |y(t)|x^{\prime}(t)dt\) の値を求めよ. ここで\(,\) \(|y(t)|\) は \(y(t)\) の絶対値\(,\) \(x^{\prime}(t)\) は \(x(t)\) の導関数を表す.
(1) の解答
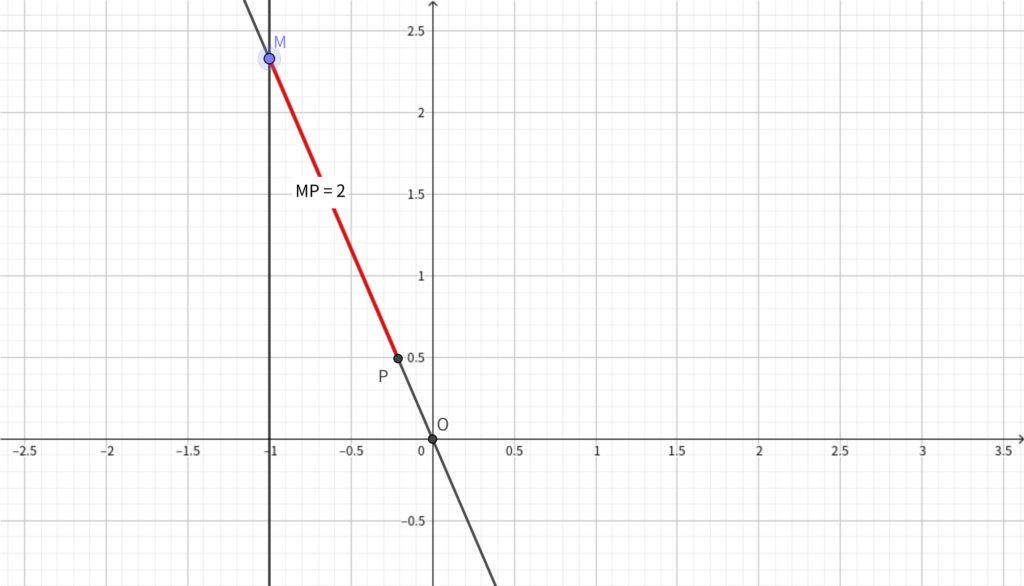
\begin{align}\mathrm{M}(-1,~\tan{t})\end{align}
\begin{align}\overrightarrow{\mathrm{PM}}=k\overrightarrow{\mathrm{OM}}~(k>0)\end{align}
とおくと\(,\) \(\left|\overrightarrow{\mathrm{PM}}\right|=2\) より\(,\)
\begin{align}{\left|\overrightarrow{\mathrm{PM}}\right|}^2=k^2{\left|\overrightarrow{\mathrm{OM}}\right|}^2\end{align}
\begin{align}4=k^2(1+\tan^2{t})\end{align}
\begin{align}4=k^2\cdot \frac{1}{\cos^2{t}}\end{align}
\begin{align}k^2=4\cos^2{t}\end{align}
\(\displaystyle k>0,~-\frac{\pi}{2}<t<\frac{\pi}{2}\) より\(,\)
\begin{align}k=2\cos{t}\end{align}
quandle
最初にベクトルを設定するときに
\begin{align}\overrightarrow{\mathrm{OM}}=k\overrightarrow{\mathrm{OP}}\end{align}
としてしまうと\(,\) \(\mathrm{P}\) が \(y\) 軸より右側に行ってしまったときに \(k\) の値は負になります. 解答のようにおくことで \(k>0\) と限定することができます.
\begin{align}\overrightarrow{\mathrm{OP}}=(1-k)\overrightarrow{\mathrm{OM}}\end{align}
\begin{align}=(1-2\cos{t})(-1,~\tan{t})\end{align}
よって\(,\)
\begin{align}\mathrm{P}(-1+2\cos{t},~\tan{t}-2\sin{t})~~~~\cdots\fbox{答}\end{align}
(2) の解答
\begin{align}\left\{\begin{array}{c}-1+2\cos{t_1}=-1+2\cos{t_2}\\ \tan{t_1}-2\sin{t_1}=\tan{t_2}-2\sin{t_2}\\ \end{array}\right. \end{align}
\begin{align}\Leftrightarrow \left\{\begin{array}{cc}\cos{t_1}=\cos{t_2} & \cdots ① \\ \tan{t_1}-2\sin{t_1}=\tan{t_2}-2\sin{t_2} & \cdots ②\\ \end{array}\right. \end{align}
\(\displaystyle -\frac{\pi}{2}<t_1 <t_2 <\frac{\pi}{2}\) であることに注意して\(,\) ①より\(,\)
\begin{align}t_2=-t_1\end{align}
このとき\(,\) ②に代入して\(,\)
\begin{align}\tan{t_1}-2\sin{t_1}=\tan{(-t_1)}-2\sin{(-t_1)}\end{align}
\begin{align}\tan{t_1}-2\sin{t_1}=-\tan{t_1}+2\sin{t_1}\end{align}
\begin{align}2\tan{t_1}=4\sin{t_1}\end{align}
\(t_1\neq 0\) より\(,\) \(2\sin{t_1}(\neq 0)\) で両辺を割ると\(,\)
\begin{align}\frac{1}{\cos{t_1}}=2\end{align}
\begin{align}\cos{t_1}=\frac{1}{2}\end{align}
したがって\(,\)
\begin{align}t_1=-\frac{\pi}{3},~t_2=\frac{\pi}{3}~~~~\cdots \fbox{答}\end{align}
quandle
ちなみにこのとき \(\mathrm{P}\) の座標は \(\mathrm{P}(0,~0)\) です.
(3) の解答
\begin{align}\left\{\begin{array}{c}x=-1+2\cos{t}\\ y=\tan{t}-2\sin{t}\end{array}\right.\end{align}
\begin{align}\frac{dx}{dt}=-2\sin{t}\end{align}
\begin{align}\frac{dy}{dt}=\frac{1}{\cos^2{t}}-2\cos{t}=\frac{1-2\cos^3{t}}{\cos^2{t}}\end{align}
\(t\neq 0\) のとき\(,\)
\begin{align}\frac{dy}{dx}=\frac{1-2\cos^3{t}}{-2\cos^2{t}\sin{t}}\end{align}
が存在するため\(,\) 接線が \(x\) 軸と直交することはない.
直交するとすれば\(,\) \(t=0\) のときであり\(,\) このとき接線は
\begin{align}x=1\end{align}
であり\(,\) 点 \(\mathrm{P}\) の座標は
\begin{align}\mathrm{P}(1,~0)~~~~\cdots \fbox{答}\end{align}
(4) の解答
(3) において \(\displaystyle \frac{dy}{dx}=0\) となるときを考える.
\begin{align}\frac{dy}{dx}=0\end{align}
\begin{align}1-2\cos^3{t}=0\end{align}
\begin{align}\cos^3{t}=\frac{1}{2}\end{align}
\begin{align}\cos{t}=\frac{1}{\sqrt[3]{2}},~\sin{t}=\pm \sqrt{1-\frac{1}{\sqrt[3]{4}}}\end{align}
このとき\(,\)
\begin{align}x=-1+\frac{2}{\sqrt[3]{2}}~~~~\cdots \fbox{答}\end{align}
\begin{align}y=\pm (\sqrt[3]{2}-2)\sqrt{1-\frac{1}{\sqrt[3]{4}}}\end{align}
であるから\(,\)
\begin{align} y ~座標の和は~ 0~~~~\cdots \fbox{答}\end{align}
(5) の着眼点
(4) で \(\displaystyle x=-1+\frac{2}{\sqrt[3]{2}}\) のとき\(,\) \(y\) の値は絶対値が等しく異符号でした.
このことから「もしかしたら \(x\) 軸対称なのでは？」と予想ができます.
媒介変数表示された曲線が \(x\) 軸対称であることを示すためには\(,\)
\(x=x(t),~y=y(t)\) に関して\(,\)
\begin{align}x(-t)=x(t),~y(-t)=-y(t)\end{align}
であることを示せばOKです.
※一般には \(x(○)=x(t),~y(○)=-y(t)\) であることを示せばOKです. 問題によっては○部分が \(-t\) であったり\(,\) \(\pi -t\) であったりします.
(5) の解答
\(x=x(t),~y=y(t)\) とおくと\(,\)
\begin{align}x(-t)=-1+2\cos{(-t)}=-1+2\cos{t}=x(t)\end{align}
\begin{align}y(-t)=\tan{(-t)}-2\sin{(-t)}=-\tan{t}+\sin{t}=-y(t)~~~~\cdots (※)\end{align}
であるから\(,\) 求める曲線は \(x\) 軸対称になる.
\(\displaystyle -\frac{\pi}{3}\leqq t \leqq \frac{\pi}{3}\) における曲線は\(,\) \(\displaystyle 0\leqq t \leqq \frac{\pi}{3}\) における曲線とそれを \(x\) 軸に関して対称に折り返した曲線を合わせたものになる. (4) で求めた \(t\) の値を \(\alpha \) とおくと\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline t & 0 & \cdots & \alpha & \cdots & \displaystyle\frac{\pi}{3}\\ \hline \displaystyle \frac{dx}{dt} & 0 & – & – & – & – \\ \hline \displaystyle \frac{dy}{dt} & – & – & 0 & + & + \\ \hline x & 1 & \leftarrow & x(\alpha ) & \leftarrow & 0 \\ \hline y & 0 & \downarrow & y(\alpha ) & \uparrow & 0 \\ \hline \end{array}\end{align}
quandle
\(\alpha \) は
\begin{align}x(\alpha )=-1+\frac{2}{\sqrt[3]{2}}\end{align}
\begin{align}y(\alpha )=(\sqrt[3]{2}-2)\sqrt{1-\frac{1}{\sqrt[3]{4}}}\end{align}
をみたす実数です.
増減表より求める曲線は以下のようになる.
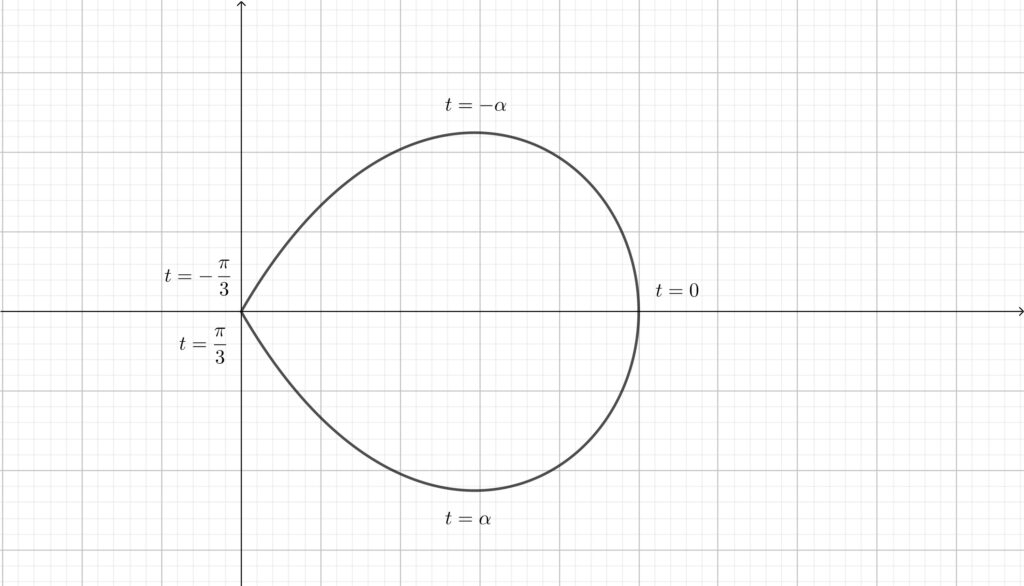原点からスタートして時計回りに１周してきて再び原点に戻ってくる曲線になります.
Geogebraによるシュミレーション
スライダーを使うことで \(-60^{\circ}\leqq t \leqq 60^{\circ}\) の範囲で \(t\) を連続的に変化させることができます.
\(t=-60^{\circ}\) のとき\(,\) 原点にあり\(,\) ここからスタートして時計回りに移動をして\(,\) \(t=60^{\circ}\) のときにまた原点に戻ってくる様子が観察できます.
(6) の着眼点
定義域が \(\displaystyle -\frac{\pi}{3}\leqq t \leqq \frac{\pi}{3}\) となっていますから\(,\) 以下の公式を利用しましょう.
\begin{align}\int_{-a}^af(x)dx=\left\{ \begin{array}{cc}0 & (f(x)~:~奇関数) \\ \displaystyle 2\int_0^af(x)dx & (f(x)~:~偶関数) \end{array}\right. \end{align}
被積分関数が奇関数か偶関数かを調べましょう.
(6) の解答
(※) より \(y(t)\) は奇関数であるから \(|y(t)|\) は偶関数である. そして\(,\)
\begin{align}x^{\prime}(t)=-2\sin{t}\end{align}
は奇関数であるから\(,\) \(|y(t)|x^{\prime}(t)\) は奇関数である. よって
\begin{align}\int_{t_1}^{t_2}|y(t)|x^{\prime}(t)dt=\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}|y(t)|x^{\prime}(t)dt=0~~~~\cdots \fbox{答}\end{align}
コメント