かなり計算量が多い問題です。いかに計算量を減らして解けるかがポイントです。
問題文全文
\(x\) の整式 \(f(x)\) が, \(x\) についての恒等式
を満たし, かつ \(f(0)=0\) であるという. ただし, \(f^{\prime}(x)\) と \(f^{\prime\prime}(x)\) はそれぞれ \(f(x)\) の第 1 次導関数と第 2 次導関数を表す. また, 文中の \(\mathrm{log}\) は自然対数を表す.
(1) 整式 \(f(x)\) の次数は \(\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) であり, \(\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) 次の項の係数は \(\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である. そして,
である.
(2) 関数 \(f(x)\)は, \(\displaystyle x=\frac{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) のとき, 極大値 \(\displaystyle \frac{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}+\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\)をとり, \(\displaystyle x=\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~,~ -\frac{\fbox{$\hskip0.8emタ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emチ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emツ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}} \) のとき, 極小値 \(\displaystyle \fbox{$\hskip0.8emテ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~, ~-\frac{\fbox{$\hskip0.8emト\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emナ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\fbox{$\hskip0.8emニ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{\fbox{$\hskip0.8emヌ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) をそれぞれとる.
(3) 曲線 \(y=f(x)\) と \(x\) 軸で囲まれた部分の面積は \(\displaystyle \frac{\fbox{$\hskip0.8emネノハ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emヒ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) である.
(1)の「次数の決定」までの着眼点
次数を求める問題です. 両辺の最高次の係数を比較することになります. 右辺が 1 次式であることはわかっています. 左辺が 1 次式以下の場合と 2 次式以上になるときで比較する最高次が変わりますから, 場合分けが発生します.
① \(f(0)=0\) という条件がありますので, \(f(x)\) の定数項は 0 であることが分かります.
② \(f(x)\) が定数関数のときは, ①により\(f(x)=0\) (すべての \(x\) に対して 0 )となりますが, 0 の次数は考えない(または \(-\infty\))とすることになっていますので題意に合いません.
③ \(f(x)=ax\) のときは, 両辺とも 1 次式になります. 両辺の 1 次の係数を比較します.
④ \(f(x)\)が \(n~(≥2)\) 次式のとき, 左辺は \(n\) 次式になりますので 「 \(n\) 次の係数=0」を解くことになります. これにより \(f(x)\) の次数が決まります.
(1)の「次数の決定」までの解答
\(f(0)=0\) より, \(f(x)\) の定数項は 0 である. このことに注意して以下の場合に分けて考える.
[1] \(f(x)=0\) のとき, 0 の次数は考えないので題意を満たさない.
[2] \(f(x)=ax~(a\neq 0)\) のとき, \(f^{\prime}(x)=a,~f^{\prime\prime}(x)=0\) であるから, 与式に代入して,
\(x\) に関する恒等式であるから, \(3a=48,~-2a=-39\) となるが, これらを同時に満たす \(a\) は存在しない.
[3] \(f(x):n~(≥2)\) 次式とし, 最高次を \(bx^n~(b\neq 0)\) とおく. このとき, \(f^{\prime}(x)=nbx^{n-1}+\cdots,~f^{\prime\prime}(x)=n(n-1)bx^{n-2}+\cdots\) となるので, 与式に代入すると,
となるので, 両辺の最高次の係数を比較すると,
より, \(n=4\) と分かる. (\(b\neq 0\) であることに注意)
(1)の積分計算の着眼点
① \(f(x)\) は定数項が 0 だったので, \(\displaystyle \frac{x}{f(x)}\) は約分されそうです.
② ①の結果分母は 3 次式になります. 因数分解して部分分数分解する流れになりそうです.
(1)の積分計算の解答
\(f(x), f^{\prime}(x), f^{\prime\prime}(x)\) を以下のようにおく.
与式に代入して,
\(x\) に関する恒等式であるから, 両辺の係数を比較して,
これを解いて, \(b=1,~c=-4,~d=-3,~e=18\) を得る.

実際に計算するときは, 最初の 3 つの式から \(c=-4b, d=-3b, e=16+2b\) とすべて \(b\) だけの式にして, 4 つ目の式 \(d-2e=-39\) に代入して求めます.
よって, \(f(x)=x^4-4x^3-3x^2+18x\) となる. このとき,

3 つ目のイコールは部分分数分解をしています. \(\displaystyle \frac{1}{(x-3)^2(x+2)}=\frac{A}{x+2}+\frac{B}{x-3}+\frac{C}{(x-3)^2}\) とおいて 通分することにより, \(A, B, C\) を求めます. ちなみに, \(\displaystyle A=\frac{1}{25}, B=-\frac{1}{25}, C=\frac{1}{5}\) となります.
(2)の解答

(2) は4次関数の極大・極小問題です. 丁寧に計算をしてミスのないようにしたいです. 特に極大値や極小値を計算するときに, 直接代入するのは大変です. 次数下げをうまく利用しましょう.
\(f^{\prime}(x)=0\) のとき, \(\displaystyle x=3,\pm\frac{\sqrt{6}}{2}\) なので, 増減表は以下のようになる.
\begin{array}{c|c|c|c|c|c|c}x & \cdots & -\frac{\sqrt{6}}{2} & \cdots & \frac{\sqrt{6}}{2} & \cdots & 3 & \cdots \\ \hline f^{\prime}(x) & – & 0 & + & 0 & – & 0 & + \\ \hline f(x) & \searrow & 極小 & \nearrow & 極大 & \searrow & 極小 & \nearrow \\ \end{array}
ここで,
であるから, \(\displaystyle x=\frac{\sqrt{6}}{2}\) のとき, 極大値 \(\displaystyle f\left(\frac{\sqrt{6}}{2}\right)=12\times \frac{\sqrt{6}}{2}-\frac{9}{4}=-\frac{9}{4}+6\sqrt{6}\)をとる.
また, \(\displaystyle x=-\frac{\sqrt{6}}{2}\) のとき, 極小値 \(\displaystyle f\left(-\frac{\sqrt{6}}{2}\right)=12\left( -\frac{\sqrt{6}}{2}\right)-\frac{9}{4}=-\frac{9}{4}-6\sqrt{6}\)をとる.

\(\displaystyle x=\pm\frac{\sqrt{6}}{2}\) は \(2x^2-3=0\) の解ですから, \(f(x)\) を\(2x^2-3\) で割ってから代入することで, 次数下げができます. こういう工夫をしないとかなりしんどい計算になります.
また, \(f(x)=x(x+2)(x-3)^2\) であるから, \(x=3\) のとき, 極小値 \(f(3)=0\) をとる.
(3)の着眼点
(2)で \(f(x)=x(x+2)(x-3)^2\) とわかったので, \(y=f(x)\) のグラフは \(x=3\) で \(x\) 軸と接することが分かります. もし \(x\) 軸が複接線であるようなら「\(\displaystyle \frac{1}{30}\) 公式」が使えるのですが, 残念ながら今回は素直に積分して面積を求めるしかなさそうです.
(3)の解答
(2) の増減表により, 求める面積は下図の斜線部分になる.
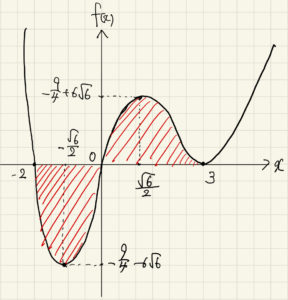
求める面積は




コメント
一見とっつきにくい問題でしたが、アプローチの方法が分かると計算できますね!
連立4元1次方程式の解を求める手順が書いてあり、助かります。求める文字の種類が増えるといつも計算量が増えすぎてしまうのが悩みでした
ごまをさん コメントありがとうございます!この問題は(1)が一番大変ですね。次数の決定、部分分数分解してからの積分計算等、1つ1つが結構重ための計算になってます。4元1次方程式の途中式なんかは解答では省略されることが多いですから、手厚く書くように心がけています。今後もよろしくお願いします!
ありがとうございます。
よろしくお願いします(o^―^o)ニコ