東京理科大学薬学部2021年第４問| 理科大の微積分

２月７日に薬学部の試験が行われました. 私立薬学部での最難関だった理科大薬学部ですが今は慶應に薬学部ができてその座を奪われてしまいました. それでも難関であることは変わりませんし$,$ 研究実績も素晴らしいです.

今回の問題は面積公式がたくさん出てきます. 使いこなせればほとんど計算せずに穴を埋めていくことができます.

微積分以外の問題についても手書きではありますが解答速報をあげておりますので合わせてご覧いただけましたら幸いです.

２月７日の薬学部を解き終えました。東進の方が早かった！東進と同じ答えになっていることは確認済です。需要ないかもですがアップしておきます。#東京理科大学　 #薬学部　 #解答速報 pic.twitter.com/O1H0Vb6Ndz
— 理科大の微積分 (@tusbiseki) February 9, 2021

問題文全文
(1) の着眼点
(1) の解答
1/30公式について
(2) の解答
２次関数と２接線の関係について
(3) の解答
(4) の着眼点
(4) の解答

問題文全文

$a,~b,~c$ を実数とする. $\displaystyle f(x)=x^4-4x^3+4x^2+\frac{1}{4}$ とする. 座標平面における曲線 $C_1~:~y=f(x)$ と放物線 $C_2~:~y=ax^2+bx+c$ は点 $\displaystyle \mathrm{P}_1~\left(\frac{2-\sqrt{2}}{2},~f\left(\frac{2-\sqrt{2}}{2}\right)\right),~\mathrm{P}_2~\left(\frac{2+\sqrt{2}}{2},~f\left(\frac{2+\sqrt{2}}{2}\right)\right)$ を共有点としてもち$,$ かつ点 $\mathrm{P}_1$ で共通の接線 $\ell_1$$,$ 点 $\mathrm{P}_2$ での共通の接線 $\ell_2$ をもつという. 曲線 $C_1$ と放物線 $C_2$ によって囲まれた部分の面積を $S_1$$,$ 接線 $\ell_1$ および $\ell_2$ と $C_2$ によって囲まれた部分の面積を $S_2$ とする.

(1) $a=-\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~,~b=\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~,~c=\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ である.

(2) $\displaystyle S_1=\frac{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emオカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}$ である.

(3) 接線 $\ell_1$ の方程式は $\displaystyle y=\sqrt{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~x+\frac{\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\sqrt{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}$ であり$,$ $\displaystyle S_2=\frac{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}$ である.

連立不等式 $\displaystyle y\geqq f(x),~y\leqq -\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~x^2+\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~x+\frac{1}{4},~x\geqq \frac{2+\sqrt{2}}{2}$ が表す領域（境界線も含む）の面積を $S_3$ とする.

(4) $\displaystyle S_3=\frac{\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emタチ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\frac{\fbox{$\hskip0.8emツ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emテトナ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8em二\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}$ である.

(1) の着眼点

$C_1$ と $C_2$ の共有点の $x$ 座標は$,$

\begin{align}x^4-4x^3+4x^2+\frac{1}{4}=ax^2+bx+c\end{align}

の解になります. $\mathrm{P}_1$ と $\mathrm{P}_2$ の座標がわかっているので$,$ この $4$ 次方程式は $\displaystyle x=\frac{2\pm \sqrt{2}}{2}$ を解にもつことが分かります.

さらに $C_1$ と $C_2$ は $\mathrm{P}_1$ と $\mathrm{P}_2$ で共通の接線をもつといっているので$,$ 重解であることも分かります.

つまり$,$ 上の $4$ 次方程式は

\begin{align}\left(x-\frac{2-\sqrt{2}}{2}\right)^2\left(x-\frac{2+\sqrt{2}}{2}\right)^2=0\end{align}

\begin{align}\Leftrightarrow \left(x^2-2x+\frac{1}{2}\right)^2=0\end{align}

とかけるはずです.

(1) の解答

$C_1$ と $C_2$ の共有点の $x$ 座標は$,$ 連立方程式

\begin{align}x^4-4x^3+4x^2+\frac{1}{4}=ax^2+bx+c\end{align}

の解である. 整理すると$,$

\begin{align}x^4-4x^3+(4-a)x^2-bx+\frac{1}{4}-c=0~~~~\cdots ①\end{align}

となる. 一方$,$ この $4$ 次方程式は条件より$,$

\begin{align}x=\frac{2-\sqrt{2}}{2},~\frac{2+\sqrt{2}}{2}\end{align}

を重解にもつから$,$

\begin{align}\left(x-\frac{2-\sqrt{2}}{2}\right)^2\left(x-\frac{2+\sqrt{2}}{2}\right)^2=0\end{align}

\begin{align}\Leftrightarrow \left(x^2-2x+\frac{1}{2}\right)^2=0\end{align}

\begin{align}\Leftrightarrow x^4+4x^2+\frac{1}{4}-4x^3-2x+x^2=0\end{align}

\begin{align}\Leftrightarrow x^4-4x^3+5x^2-2x+\frac{1}{4}=0~~~~\cdots ②\end{align}

とかける. ①と②は恒等式として等しいので$,$

\begin{align}4-a=5,~b=2,~\frac{1}{4}-c=\frac{1}{4}\end{align}

\begin{align}a=-1,~b=2,~c=0~~~~\cdots \fbox{答}\end{align}

ア：１　イ：２　ウ：０

1/30公式について

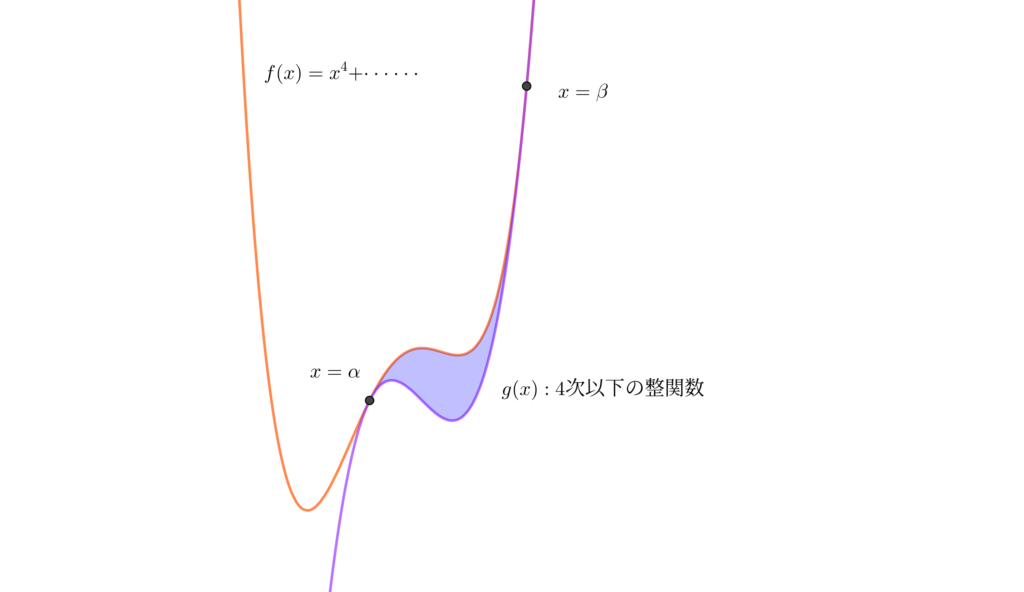
上の図のように $,$ $4$ 次関数のグラフと $4$ 次以下の整関数のグラフが $x=\alpha$ と $x=\beta$ の $2$ 点で接するとき$,$ $2$ つの曲線で囲まれる部分の面積 $S$ は

$\displaystyle S=\int_{\alpha}^{\beta}(x-\alpha)^2(x-\beta)^2dx=-\frac{1}{30}(\beta -\alpha)^5$

で求められます. これは $1$/$30$ 公式と呼ばれています.

注：どちらも $4$ 次関数の場合は $4$ 次の係数が異なる場合に限ります.

(2) の解答

\begin{align}S_1=\int_{\frac{2-\sqrt{2}}{2}}^{\frac{2+\sqrt{2}}{2}}\left\{x^4-4x^3+4x^2+\frac{1}{4}-\left(-x^2+2x\right)\right\}dx\end{align}

\begin{align}=\int_{\frac{2-\sqrt{2}}{2}}^{\frac{2+\sqrt{2}}{2}}\left(x-\frac{2-\sqrt{2}}{2}\right)^2\left(x-\frac{2+\sqrt{2}}{2}\right)^2dx\end{align}

\begin{align}=\frac{1}{30}\left(\frac{2+\sqrt{2}}{2}-\frac{2-\sqrt{2}}{2}\right)^5=\frac{2}{15}\sqrt{2}~~~~\cdots \fbox{答}\end{align}

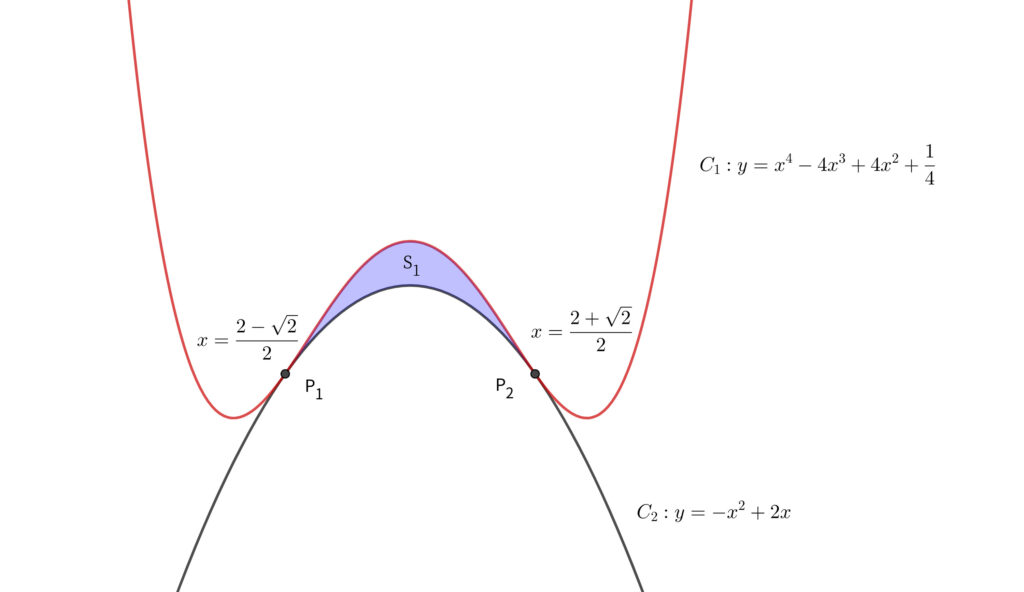
エ：２　オ：１　カ：５　キ：２

２次関数と２接線の関係について

２次関数と２接線によって囲まれる面積は $\displaystyle \frac{1}{12}$ 公式を利用すれば瞬殺できます.

2 次関数 $C~:~y=ax^2+\cdots$ と $C$ の$x=\alpha$ における接線 $\ell_1$, $x=\beta$ における接線 $\ell_2$ で囲まれる部分の面積 $S_1$ は

\begin{align}S_1=\frac{|a|}{12}(\beta -\alpha)^3\end{align}

で求められます.

詳しくは下の記事で $2$ 次関数と $2$ 接線の関係についてまとめていますので合わせてご覧いただければと思います.

理学部（数・物・化）2020年第２問

東京理科大学の数学の過去問のうち、理学部（数学科・物理学科・化学科）の２０２０年第２問を解説しています。

(3) の解答

$C_2~:~y=-x^2+2x$ において$,$ $\displaystyle x=\frac{2-\sqrt{2}}{2}$ のとき

\begin{align}y=-\left(\frac{2-\sqrt{2}}{2}\right)^2+2\cdot \frac{2-\sqrt{2}}{2}\end{align}

\begin{align}=-\frac{6-2\sqrt{2}}{4}+2-\sqrt{2}=\frac{1}{2}\end{align}

よって$,$ 接点 $\mathrm{P}_1$ の座標は

\begin{align}\mathrm{P}_1=\left(\frac{2-\sqrt{2}}{2},~\frac{1}{2}\right)\end{align}

である. また$,$ $y^{\prime}=-2x+2$ であるから$,$ 接線 $\ell_1$ は

\begin{align}\ell_1~:~y=\left(-2\cdot \frac{2-\sqrt{2}}{2}+2\right)\left(x-\frac{2-\sqrt{2}}{2}\right)+\frac{1}{2}\end{align}

\begin{align}y=\sqrt{2}x-\sqrt{2}\cdot \frac{2-\sqrt{2}}{2}+\frac{1}{2}\end{align}

\begin{align}\ell_1~:~y=\sqrt{2}x+\frac{3}{2}-\sqrt{2}~~~~\cdots \fbox{答}\end{align}

更に$,$

\begin{align}S_2=\frac{1}{12}\left(\frac{2+\sqrt{2}}{2}-\frac{2-\sqrt{2}}{2}\right)^3=\frac{1}{6}\sqrt{2}~~~~\cdots \fbox{答}\end{align}

quandle

$\displaystyle \frac{1}{12}$ 公式は$,$ 接点の $x$ 座標さえ分かれば使えます.

今回は穴埋め式ですから$,$ $\ell_2$ すら求めずに公式に代入するだけで瞬殺できます.

ク：２　ケ：３　コ：２　サ：２　シ：１　ス：６　セ：２

(4) の着眼点

面積を求める問題の場合必ずしも正確なグラフをかく必要はありません. $2$ つのグラフの上下関係と交点さえわかれば面積を求めることができます.

$\displaystyle y=-x^2+2x+\frac{1}{4}$ のグラフは $C_2$ を $y$ 軸方向に $\displaystyle \frac{1}{4}$ だけ平行移動したものになっています.

また$,$

\begin{align}x^4-4x^3+4x^2+\frac{1}{4}=-x^2+2x+\frac{1}{4}\end{align}

\begin{align}\Leftrightarrow x(x-1)^2(x-2)=0\end{align}

であることから$,$ $x=1$ で接し$,$ かつ $x=0,~x=2$ で交わることが分かります.

このくらいの情報があればグラフの位置関係はつかめます. わざわざ増減表を書く必要はありません.

(4) の解答

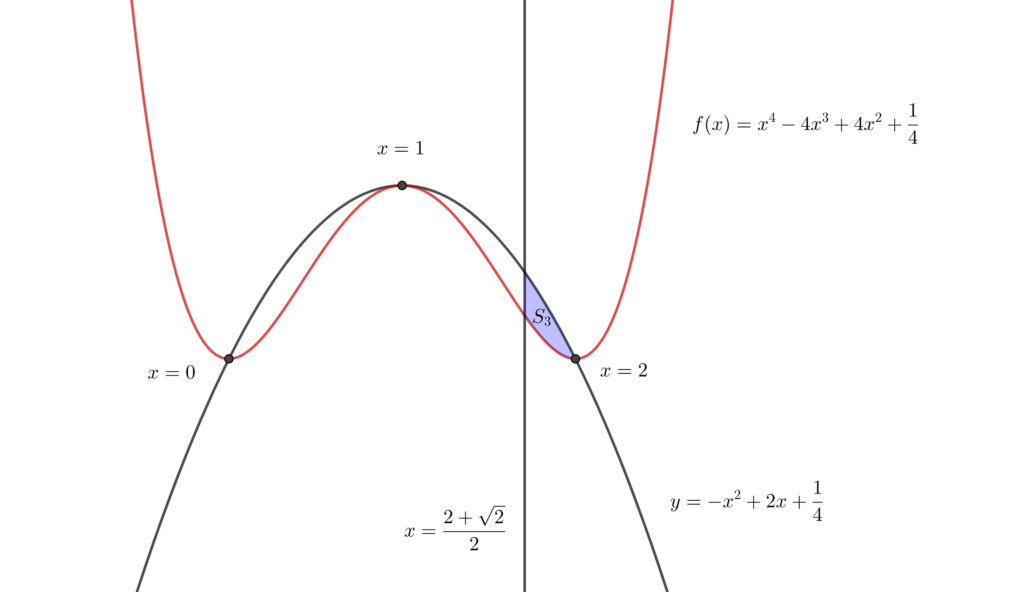
上図のようになるので$,$ 求める面積 $S_3$ は

\begin{align}S_3=\int_{\frac{2+\sqrt{2}}{2}}^2\left\{\left(-x^2+2x+\frac{1}{4}\right)-\left(x^4-4x^3+4x^2+\frac{1}{4}\right)\right\}dx\end{align}

\begin{align}=\int_{\frac{2+\sqrt{2}}{2}}^2(-x^4+4x^3-5x^2+2x)dx\end{align}

ここで$,$ $\displaystyle F(x)=-\frac{1}{5}x^5+x^4-\frac{5}{3}x^3+x^2$ とおくと$,$

\begin{align}S_3=\biggl[F(x)\biggr]_{\frac{2+\sqrt{2}}{2}}^2=F(2)-F\left(\frac{2+\sqrt{2}}{2}\right)\end{align}

\begin{align}=-\frac{32}{5}+16-\frac{40}{3}+4-F\left(\frac{2+\sqrt{2}}{2}\right)=\frac{4}{15}-F\left(\frac{2+\sqrt{2}}{2}\right)\end{align}

quandle

$\displaystyle F\left(\frac{2+\sqrt{2}}{2}\right)$ をどうやって計算するかを考えます. $5$ 次式ですから思考停止で代入するわけにはいかないのは明白です.こういうときは次数下げを考えるのがセオリーです.

$\displaystyle x=\frac{2+\sqrt{2}}{2}$ は $2x-2=\sqrt{2}$ と変形して整理することで$,$ $\displaystyle x^2-2x+\frac{1}{2}=0$ の解であることが分かります.

$F(x)$ を$\displaystyle x^2-2x+\frac{1}{2}$ で割ることにより$,$ $1$ 次式まで次数を下げることができます. $1$ 次式であれば代入は容易です.

\begin{align}F(x)=\left(x^2-2x+\frac{1}{2}\right)\left(-\frac{1}{5}x^3+\frac{3}{5}x^2-\frac{11}{30}x-\frac{1}{30}\right)+\frac{7}{60}x+\frac{1}{60}\end{align}

であることから$,$

\begin{align}F\left(\frac{2+\sqrt{2}}{2}\right)=\frac{7}{60}\cdot \frac{2+\sqrt{2}}{2}+\frac{1}{60}\end{align}

\begin{align}=\frac{2}{15}+\frac{7}{120}\sqrt{2}\end{align}

以上より$,$

\begin{align}S_3=\frac{4}{15}-\left(\frac{2}{15}+\frac{7}{120}\sqrt{2}\right)\end{align}

\begin{align}=\frac{2}{15}-\frac{7}{120}\sqrt{2}~~~~\cdots \fbox{答}\end{align}

ソ：２　タ：１　チ：５　ツ：７　テ：１　ト：２　ナ：０　二：２