問題文全文
\begin{align}S(a)=\int_0^{\frac{\pi}{2}}|a\cos{x}-\sin{x}|dx~~(a>0)\end{align}
とするとき\(,\)
\begin{align}S(\sqrt{3})=\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}-\sqrt{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
であり\(,\) 一般に
\begin{align}S(a)=\sqrt{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~a^2+~\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-(~\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~a+~\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~)\end{align}
となる.
着眼点 〜\(S(a)\) を先に求める〜
① 被積分関数に絶対値がついています. 中身が＋のときとーのときで場合分けする必要がありそうです.
② 絶対値の中身が \(\sin \) と \(\cos \) の \(1\) 次式になっています. 合成して \(\sin \) だけで表しましょう.
③ \(S(\sqrt{3})\) を聞いた後に\(,\) \(S(a)\) を聞かれています. どちらの計算も大きな差はなさそうです. 素直に \(S(\sqrt{3})\) から計算すると二度手間になるので\(,\) 先に \(S(a)\) を求めましょう.
\(S(a)\) の式に \(a=\sqrt{3}\) を代入するほうが問題全体にかかる時間は速そうです.
解答
\begin{align}S(a)=\int_0^{\frac{\pi}{2}}|\sin{x}-a\cos{x}|dx\end{align}
\begin{align}=\sqrt{a^2+1}\int_0^{\frac{\pi}{2}}|\sin{(x-\alpha )}|dx \end{align}
\begin{align}\left(ただし,~\alpha ~は ~\sin{\alpha}=\frac{a}{\sqrt{a^2+1}},~\cos{\alpha}=\frac{1}{\sqrt{a^2+1}} をみたす鋭角\right)\end{align}
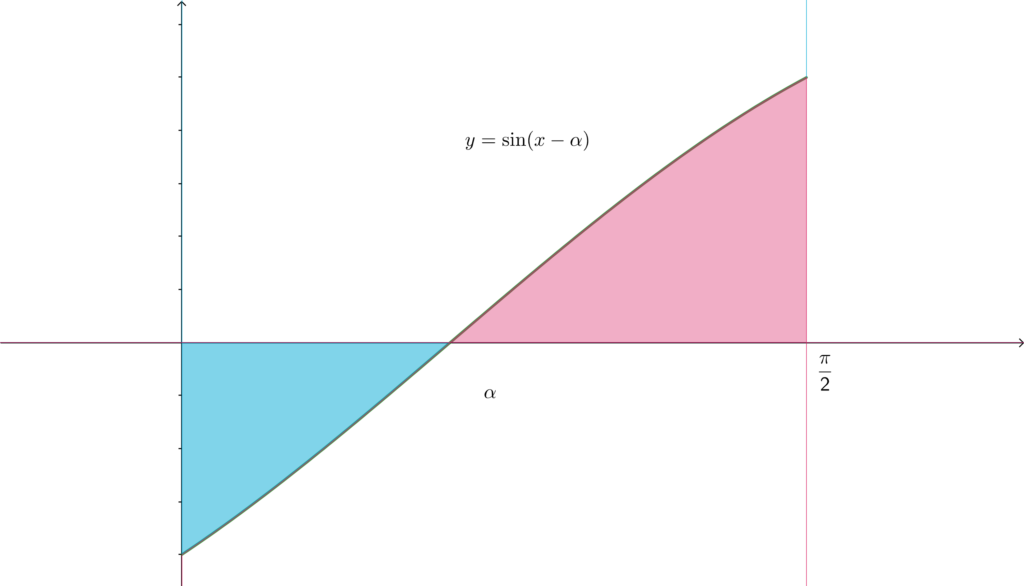
\begin{align}=\sqrt{a^2+1}\left\{\int_0^{\alpha}-\sin{(x-\alpha )}dx+\int_{\alpha}^{\frac{\pi}{2}}\sin{(x-\alpha )}dx\right\}\end{align}
\begin{align}=\sqrt{a^2+1}\left\{\biggl[\cos{(x-\alpha )}\biggr]_0^{\alpha}+\biggl[-\cos{(x-\alpha )}\biggr]_{\alpha}^{\frac{\pi}{2}}\right\}\end{align}
\begin{align}=\sqrt{a^2+1}\left[(1-\cos{\alpha})+\left\{-\cos{\left(\frac{\pi}{2}-\alpha \right)}+1\right\}\right]\end{align}
\begin{align}=\sqrt{a^2+1}(2-\cos{\alpha}-\sin{\alpha})=\sqrt{a^2+1}\left(2-\frac{1}{\sqrt{a^2+1}}-\frac{a}{\sqrt{a^2+1}}\right)\end{align}
\begin{align}=2\sqrt{a^2+1}-(a+1)=\sqrt{4a^2+4}-(a+1)~~~~\cdots \fbox{答}\end{align}
\(a=\sqrt{3}\) のとき\(,\)
\begin{align}S(\sqrt{3})=\sqrt{4\cdot 3+4}-(\sqrt{3}+1)=3-\sqrt{3}~~~~\cdots \fbox{答}\end{align}
ケ：３ コ：３ サ：４ シ：４ ス：１ セ：１
コメント