東京理科大学理学部第二部2023年第６問

理【二部】

2023.08.05

理学部第二部2023年第６問の問題文全文
(1) の解答〜代入するだけなので確実に〜
(2) の解答〜 $b(t)$ は $2$ 次関数〜
(3) の解答〜(1) からグラフの概形がすぐわかる〜

理学部第二部2023年第６問の問題文全文

$t$ を$t>0$ を満たす実数とし$,$ 関数 $f(x)$ を

\begin{align}f(x)=x^3+(t-2)x^2-2t(t+1)x+4t^2\end{align}

で定める.

(1) $f(t)=~\fbox{$\hskip0.4emそ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$},~f(2)=~\fbox{$\hskip0.4emた\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}$ である.

(2) 曲線 $y=f(x)$ 上の点 $(2,~f(2))$ における接線を ${\ell}_t$ とする. 接線 ${\ell}_t$ と $y$ 軸の交点を $(0,~b(t))$ とするとき$,$ $b(t)$ は $\displaystyle t=\frac{~\fbox{$\hskip0.4emち\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~} {~\fbox{$\hskip0.4emつ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}$ のとき最小値 $-~\fbox{$\hskip0.4emて\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}$ をとる. また$,$ $t$ が $\displaystyle \frac{1}{\sqrt{5}}\leqq t \leqq 3$ の範囲で動くとき$,$ $b(t)$ は $t=~\fbox{$\hskip0.4emと\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}$ のとき最大値 $\fbox{$\hskip0.4emなに\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}$ をとる.

(3) $t>2$ のとき$,$ 曲線 $y=f(x)$ および $x$ 軸で囲まれた領域と$,$ 連立不等式 $x\geqq 2,~x\leqq t$ の表す領域の共通部分の面積を $S(t)$ とすると$,$

\begin{align}\lim_{t\to \infty}\frac{S(t)}{t^4}=\frac{~\fbox{$\hskip0.4emぬ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emねの\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}

である.

(1) の解答〜代入するだけなので確実に〜

\begin{align}f(t)=t^3+(t-2)t^2-2t(t+1)t+4t^2=0~~~~\cdots \fbox{答}\end{align}

\begin{align}f(2)=8+4(t-2)-4t(t+1)+4t^2=0~~~~\cdots \fbox{答}\end{align}

quandle

$f(t)=0,~f(2)=0$ ということは因数定理から $(x-t)(x-2)$ を因数にもつことがわかりますね. あとは $x^3$ の係数が $1$ であることと$,$ 定数項が $4t^2$ であることから$,$

\begin{align}f(x)=(x-t)(x-2)(x+2t)\end{align}

であることが確定しますね. (1) からここまでの情報を引き出せておけば完璧です！

そ：０　た：０

(2) の解答〜 $b(t)$ は $2$ 次関数〜

\begin{align}f^{\prime}(x)=3x^2+2(t-2)x-2t(t+1)\end{align}

$f^{\prime}(2)=12+4t-8-2t^2-2t=-2t^2+2t+4$ より$,$

\begin{align}{\ell}_t~:~y=(-2t^2+2t+4)(x-2)\end{align}

$x=0$ のとき$,$

\begin{align}b(t)=4t^2-4t-8=4\left(t-\frac{1}{2}\right)^2-9\end{align}

$t>0$ より$,$

\begin{align} t=\frac{1}{2}~ のとき最小値~-9~~~~\cdots \fbox{答}\end{align}

$\displaystyle \frac{1}{\sqrt{5}}\leqq t \leqq 3$ より$,$

\begin{align} t=3~のとき最大値~b(3)=36-12-8=16~~~~\cdots \fbox{答}\end{align}

である.

quandle

$\displaystyle \frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$ で$,$ $\sqrt{5}$ が 2.2 くらいなので$,$ $\displaystyle \frac{1}{\sqrt{5}}=0.44$ くらいです. 軸である $\displaystyle x=\frac{1}{2}=0.5$ は定義域のかなり左側にあることがわかりますね.

ち：１　つ：２　て：９　と：３　な：１　に：６

(3) の解答〜(1) からグラフの概形がすぐわかる〜

(1) より$,$

\begin{align}f(x)=(x+2t)(x-2)(x-t)\end{align}

であり$,$ $t>2$ より$,$ $-2t<2<t$ であるから$,$ グラフの概形は以下のようになる.

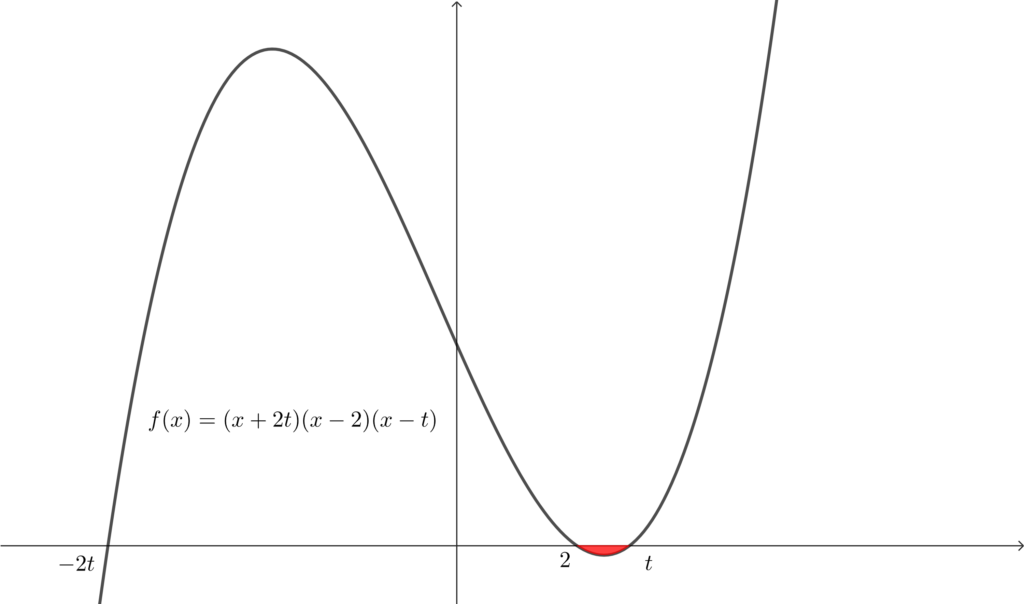
上図の赤色部分の面積を求めればよい.

\begin{align}S(t)=\int_2^t\{-x^3-(t-2)x^2+2t(t+1)x-4t^2\}dx\end{align}

\begin{align}=\biggl[-\frac{1}{4}x^4-\frac{t-2}{3}x^3+t(t+1)x^2-4t^2x\biggr]_2^t\end{align}

\begin{align}=-\frac{1}{4}t^4-\frac{1}{3}t^4+\frac{2}{3}t^3+t^4+t^3-4t^3-\left(-4-\frac{8}{3}t+\frac{16}{3}+4t^2+4t-8t^2\right)\end{align}

\begin{align}=\frac{5}{12}t^4-\frac{7}{3}t^3+4t^2-\frac{4}{3}t-\frac{4}{3}\end{align}

\begin{align}\lim_{t\to \infty}\frac{S(t)}{t^4}=\lim_{t\to \infty}\left(\frac{5}{12}-\frac{7}{3t}+\frac{4}{t^2}-\frac{4}{3t^3}-\frac{4}{3t^4}\right)\end{align}

\begin{align}=\frac{5}{12}~~~~\cdots \fbox{答}\end{align}

ぬ：５　ね：１　の：２