東京理科大学薬学部2023年第２問

薬学部2023年第２問の問題文全文
(1)(a) の解答
1. 直線 $\ell $ の方程式を求める〜「通る点」と「傾き」〜
2. $u,~v$ を $t$ で表す〜一文字消去する〜
(1) (b) の解答
1. $t$ を $\theta $ で表す〜直線の傾きはなす角の $\tan$〜
2. $\displaystyle \frac{dt}{d\theta}$ を求める〜相互関係の利用〜
(2) の解答
補足〜三角関数の有理関数の積分〜

薬学部2023年第２問の問題文全文

(1) $u=\cos{\theta},~v=\sin{\theta}~(0\leqq \theta <\pi)$ とする. 点 $(-1,~0)$ と $(u,~v)$ を通る直線を $\ell $ とし$,$ $\ell $ の傾きを $t$ とする.

(a) 直線 $\ell $ の方程式は $y=t(x+~\fbox{$\hskip0.4emア\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~)$ である. また$,$ $u,~v$ を $t$ を用いて表すと

\begin{align}u=\frac{~\fbox{$\hskip0.4emイ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~-t^2~}{~\fbox{$\hskip0.4emウ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~+t^2~}~,~v=\frac{~\fbox{$\hskip0.4emエ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~t~}{~\fbox{$\hskip0.4emオ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~+t^2~}\end{align}

である.

(b) $t$ を $\theta $ を用いて表すと

\begin{align}t=\tan{\left(\frac{~\fbox{$\hskip0.4emカ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emキ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\theta \right)}\end{align}

である. したがって$,$

\begin{align}\frac{d\theta}{dt}=\frac{~\fbox{$\hskip0.4emク\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emケ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~+t^2~}\end{align}

となる.

(2) $\log $ を自然対数とする. このとき$,$

\begin{align}\int_0^{\frac{\pi}{2}}\frac{1}{5+4\sin{x}+3\cos{x}}dx=\frac{~\fbox{$\hskip0.4emコ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emサ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}

であり$,$

\begin{align}\int_0^{\frac{\pi}{3}}\frac{1}{1+\sin{x}+\cos{x}}dx=\log{\left(~\fbox{$\hskip0.4emシ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~+~\frac{~\fbox{$\hskip0.4emス\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emセ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\sqrt{~\fbox{$\hskip0.4emソ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\right)}\end{align}

である. また$,$

\begin{align}\int_0^{\frac{\pi}{4}}\frac{\sin{x}}{\sin{x}+\cos{x}}dx=\frac{~\fbox{$\hskip0.4emタ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emチ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\pi -~\frac{~\fbox{$\hskip0.4emツ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emテ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\log{2},\end{align}

\begin{align}\int_0^{\frac{\pi}{4}}\frac{\cos{x}}{\sin{x}+\cos{x}}dx=\frac{~\fbox{$\hskip0.4emト\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emナ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\pi +~\frac{~\fbox{$\hskip0.4emニ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emヌ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\log{2},\end{align}

である.

(1)(a) の解答

直線 $\ell $ の方程式を求める〜「通る点」と「傾き」〜

直線 $\ell $ は $(-1,~0)$ を通り$,$ 傾き $t$ の直線であるから$,$

\begin{align}\ell ~:~y=t(x+1)~~~~\cdots \fbox{答}\end{align}

ア：１

$u,~v$ を $t$ で表す〜一文字消去する〜

三角関数の相互関係より$,$

\begin{align}u^2+v^2=1\end{align}

また$,$ $(u,~v)$ は直線 $\ell $ 上の点であるから$,$

\begin{align}v=t(u+1)\end{align}

\begin{align}v^2=t^2(u+1)^2\end{align}

\begin{align}1-u^2=t^2(u+1)^2\end{align}

$0\leqq \theta <\pi $ より$,$ $1+u\neq 0$ であるから$,$ 両辺を $1+u$ で割って$,$

\begin{align}1-u=t^2(u+1)\end{align}

\begin{align}(t^2+1)u=1-t^2\end{align}

$1+t^2>0$ より$,$

\begin{align}u=\frac{1-t^2}{1+u^2}~~~~\cdots \fbox{答}\end{align}

quandle

未知数は $t,~u,~v$ の $3$ つですので式が $2$ つあれば $t$ だけで表すことができます. $1$ つは $\ell $ 上の点という条件からすぐに出ますが$,$ $2$ つ目の式は自分で持ってこないといけません.相互関係はいつでも成り立つ性質ですので相互関係を引っ張り出して来ています.

$v=t(1+u)$ に代入して$,$

\begin{align}v=t\cdot \frac{1-t^2+1+t^2}{1+t^2}=\frac{2t}{1+t^2}~~~~\cdots \fbox{答}\end{align}

イ：１　ウ：１　エ：２　オ：１

(1) (b) の解答

$t$ を $\theta $ で表す〜直線の傾きはなす角の $\tan$〜

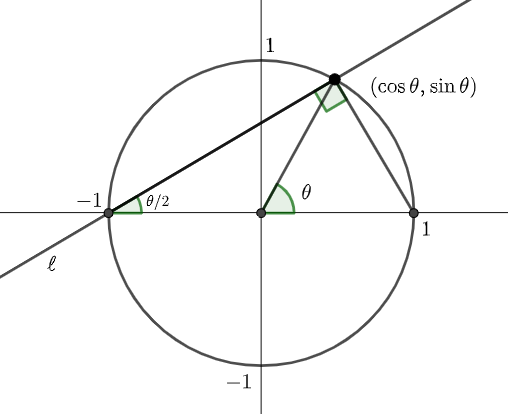
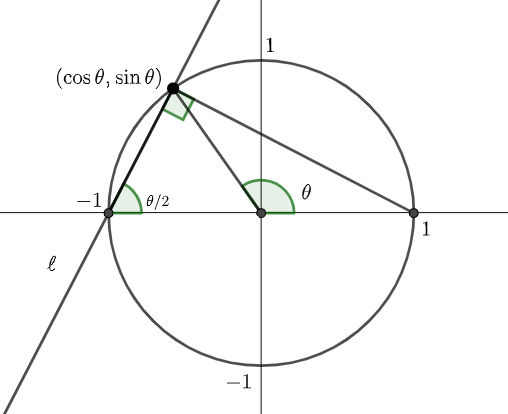
$(\cos{\theta},~\sin{\theta})$ は円 $x^2+y^2=1$ 上の点であるから$,$ 下図のような位置関係になる.

左図は $\theta$ が鋭角の場合$,$ 右図は $\theta $ が鈍角の場合の図であるが$,$ どちらの場合も円周角の定理により$,$ 直線 $\ell $ と $x$ 軸の正の向きとのなす角は $\displaystyle \frac{\theta}{2}$ で表される. これは $\displaystyle \theta =0,~\frac{\pi}{2} $ のときも成り立つ.

直線 $\ell $ の傾きは $\ell $ と $x$ 軸の正の向きとのなす角の正接の値に等しいので$,$

\begin{align}t=\tan{\left(\frac{1}{2}\theta\right)}~~~~\cdots \fbox{答}\end{align}

カ：１　キ：２

$\displaystyle \frac{dt}{d\theta}$ を求める〜相互関係の利用〜

\begin{align}\frac{dt}{d\theta}=\cfrac{1}{2\cos^2{\cfrac{\theta}{2}}}\end{align}

\begin{align}=\frac{1}{2}\left(1+\tan^2{\frac{\theta}{2}}\right)=\frac{1+t^2}{2}\end{align}

\begin{align}\therefore \frac{d\theta}{dt}=\cfrac{1}{\cfrac{dt}{d\theta}}=\frac{2}{1+t^2}~~~~\cdots \fbox{答}\end{align}

ク：２　ケ：１

(2) の解答

$\displaystyle \int_0^{\frac{\pi}{2}}\frac{1}{5+4\sin{x}+3\cos{x}}dx$ を求める〜有理関数に変形〜

$\displaystyle t=\tan{\frac{x}{2}}$ とおくと$,$

\begin{align}\begin{array}{|c|ccc|}\hline x & 0 & \to & \displaystyle \frac{\pi}{2}\\ \hline t & 0 & \to & 1 \\ \hline \end{array}\end{align}

であるから$,$ (1) で求めた置換と合わせて$,$ 与式は以下のように置換積分できる.

\begin{align}\int_0^{\frac{\pi}{2}}\frac{1}{5+4\sin{x}+3\cos{x}}dx=\int_0^1\cfrac{\cfrac{2}{1+t^2}}{5+4\cdot \cfrac{2t}{1+t^2}+3\cdot \cfrac{1-t^2}{1+t^2}}dt\end{align}

\begin{align}=\int_0^1\frac{2}{5(1+t^2)+8t+3(1-t^2)}dt=\int_0^1\frac{2}{2t^2+8t+8}dt\end{align}

\begin{align}=\int_0^1\frac{1}{(t+2)^2}dt=\biggl[-\frac{1}{t+2}\biggr]_0^1\end{align}

\begin{align}=-\frac{1}{3}+\frac{1}{2}=\frac{1}{6}~~~~\cdots \fbox{答}\end{align}

コ：１　サ：６

$\displaystyle \int_0^{\frac{\pi}{3}}\frac{1}{1+\sin{x}+\cos{x}}dx$ を求める〜これも有理関数に変形〜

\begin{align}\begin{array}{|c|ccc|}\hline x & 0 & \to & \displaystyle \frac{\pi}{3}\\ \hline t & 0 & \to & \displaystyle \frac{1}{\sqrt{3}}\\ \hline \end{array}\end{align}

より$,$ 与式は以下のように置換積分できる.

\begin{align}\int_0^{\frac{\pi}{3}}\frac{1}{1+\sin{x}+\cos{x}}dx=\int_0^{\frac{1}{\sqrt{3}}}\cfrac{\cfrac{2}{1+t^2}}{1+\cfrac{2t}{1+t^2}+\cfrac{1-t^2}{1+t^2}}dt\end{align}

\begin{align}=\int_0^{\frac{1}{\sqrt{3}}}\frac{2}{1+t^2+2t+1-t^2}dt=\int_0^{\frac{1}{\sqrt{3}}}\frac{1}{t+1}dt\end{align}

\begin{align}=\biggl[\log{|t+1|}\biggr]_0^{\frac{1}{\sqrt{3}}}=\log{\left(1+\frac{1}{3}\sqrt{3}\right)}~~~~\cdots \fbox{答}\end{align}

シ：１　ス：１　セ：３　ソ：３

$\displaystyle I=\int_0^{\frac{\pi}{4}}\frac{\sin{x}}{\sin{x}+\cos{x}}dx$ と $\displaystyle J=\int_0^{\frac{\pi}{4}}\frac{\cos{x}}{\sin{x}+\cos{x}}dx$ を同時に求める〜 $I+J$ と $I-J$ を計算する〜

\begin{align}I=\int_0^{\frac{\pi}{4}}\frac{\sin{x}}{\sin{x}+\cos{x}}dx,~J=\int_0^{\frac{\pi}{4}}\frac{\cos{x}}{\sin{x}+\cos{x}}dx\end{align}

とおく.

\begin{align}I+J=\int_0^{\frac{\pi}{4}}dx\end{align}

\begin{align}=\bigl[x\bigr]_0^{\frac{\pi}{4}}=\frac{\pi}{4}~~~~\cdots ①\end{align}

\begin{align}I-J=\int_0^{\frac{\pi}{4}}\frac{\sin{x}-\cos{x}}{\sin{x}+\cos{x}}dx\end{align}

\begin{align}=\int_0^{\frac{\pi}{4}}-\frac{(\sin{x}+\cos{x})^{\prime}}{\sin{x}+\cos{x}}dx=\biggl[-\log{|\sin{x}+\cos{x}|}\biggr]_0^{\frac{\pi}{4}}\end{align}

\begin{align}=-\log{\sqrt{2}}=-\frac{1}{2}\log{2}~~~~\cdots ②\end{align}

$\displaystyle \frac{1}{2}(①+②)$ より$,$

\begin{align}I=\frac{1}{8}\pi-\frac{1}{4}\log{2}~~~~\cdots \fbox{答}\end{align}

$\displaystyle \frac{1}{2}(①-②)$ より$,$

\begin{align}J=\frac{1}{8}\pi+\frac{1}{4}\log{2}~~~~\cdots \fbox{答}\end{align}

タ：１　チ：８　ツ：１　テ：４　ト：１　ナ：８　ニ：１　ヌ：４

$I$ の別解〜有理関数にして無理やり計算〜

\begin{align}\begin{array}{|c|ccc|}\hline x & 0 & \to & \displaystyle \frac{\pi}{4}\\ \hline t & 0 & \to & \sqrt{2}-1\\ \hline \end{array}\end{align}

より$,$ $I$ は以下のように置換積分できる.

quandle

$t$ の範囲を求めるときに$,$ $\displaystyle \tan{\frac{\pi}{8}}$ を求める必要があります. 詳細は割愛しますが$,$ 半角の公式を用いることで$,$ $\displaystyle \tan{\frac{\pi}{8}}=\sqrt{2}-1$ が求められます. 分母の有理化や二重根号を外す変形があるので$,$ これだけでも結構計算力が必要です.

\begin{align}I=\int_0^{\frac{\pi}{4}}\frac{\sin{x}}{\sin{x}+\cos{x}}dx\end{align}

\begin{align}=\int_0^{\sqrt{2}-1}\cfrac{\cfrac{2t}{1+t^2}}{\cfrac{2t}{1+t^2}+\cfrac{1-t^2}{1+t^2}}\cdot \frac{2}{1+t^2}dt\end{align}

\begin{align}=\int_0^{\sqrt{2}-1}\frac{4t}{(2t+1-t^2)(1+t^2)}dt=\int_0^{\sqrt{2}-1}\left(\frac{t-1}{-t^2+2t+1}+\frac{t+1}{t^2+1}\right)dt\end{align}

quandle

詳細は割愛しますが部分分数分解をしています.

\begin{align}\frac{At+B}{-t^2+2t+1}+\frac{Ct+D}{t^2+1}\end{align}

として$,$ $A,~B,~C,~D$ を求めればOKです.

\begin{align}=\int_0^{\sqrt{2}-1}\left(-\frac{1}{2}\cdot \frac{-2t+2}{-t^2+2t+1}+\frac{1}{2}\cdot \frac{2t}{t^2+1}\right)dt+\int_0^{\sqrt{2}-1}\frac{1}{t^2+1}dt\end{align}

\begin{align}K=\int_0^{\sqrt{2}-1}\left(-\frac{1}{2}\cdot \frac{-2t+2}{-t^2+2t+1}+\frac{1}{2}\cdot \frac{2t}{t^2+1}\right)dt,~L=\int_0^{\sqrt{2}-1}\frac{1}{t^2+1}dt\end{align}

とおく.

\begin{align}K=\biggl[-\frac{1}{2}\log{|-t^2+2t+1|}+\frac{1}{2}\log{|t^2+1|}\biggr]_0^{\sqrt{2}-1}\end{align}

\begin{align}=-\frac{1}{2}\log{(4\sqrt{2}-4)}+\frac{1}{2}\log{(4-2\sqrt{2})}=\frac{1}{2}\log{\frac{4-2\sqrt{2}}{4\sqrt{2}-4}}\end{align}

\begin{align}=\frac{1}{2}\log{\frac{2-\sqrt{2}}{2\sqrt{2}-2}}=\frac{1}{2}\log{\frac{(2-\sqrt{2})(2\sqrt{2}+2)}{8-4}}=-\frac{1}{4}\log{2}\end{align}

$t=\tan{\varphi}$ とおくと$,$ $\displaystyle dt=\frac{1}{\cos^2{\varphi}}d\varphi$ であり$,$

\begin{align}\begin{array}{|c|ccc|}\hline t & 0 & \to & \sqrt{2}-1 \\ \hline \varphi & 0 & \to & \displaystyle \frac{\pi}{8}\\ \hline \end{array}\end{align}

であるから$,$ $L$ は以下のように置換積分できる.

\begin{align}L=\int_0^{\frac{\pi}{8}}\frac{1}{\tan^2{\varphi}+1}\cdot \frac{1}{\cos^2{\varphi}}d\varphi\end{align}

\begin{align}=\int_0^{\frac{\pi}{8}}d\varphi=\bigl[\varphi\bigr]_0^{\frac{\pi}{8}}=\frac{\pi}{8}\end{align}

以上より$,$

\begin{align}I=K+L=\frac{1}{8}\pi-\frac{1}{4}\log{2}~~~~\cdots \fbox{答}\end{align}

$J$ の別解〜有理関数にして無理やり計算〜

\begin{align}J=\int_0^{\frac{\pi}{4}}\frac{\cos{x}}{\sin{x}+\cos{x}}dx\end{align}

\begin{align}=\int_0^{\sqrt{2}-1}\cfrac{\cfrac{1-t^2}{1+t^2}}{\cfrac{2t}{1+t^2}+\cfrac{1-t^2}{1+t^2}}\cdot \frac{2}{1+t^2}dt=\int_0^{\sqrt{2}-1}\frac{2-2t^2}{(2t+1-t^2)(1+t^2)}dt\end{align}

\begin{align}=\int_0^{\sqrt{2}-1}\left(\frac{-t+1}{-t^2+2t+1}+\frac{-t+1}{t^2+1}\right)dt\end{align}

\begin{align}=-M+L=\frac{1}{8}\pi-\frac{1}{4}\log{2}~~~~\cdots \fbox{答}\end{align}