薬学部2024年第4問の問題文全文
\(n\)を自然数とし\(,\) 関数
\begin{align}f_n(x)=x^{-n}\log{x}~(x>0)\end{align}
とする. 座標平面上の曲線 \(C~:~y=f_n(x)\) 上の点 \((a,~f_n(a))\) における接線 \(\ell \) が\(,\) 座標平面の原点を通るという. ただし\(,\) \(\log{}\) は自然対数を表し\(,\) 文中の \(e\) は自然対数の底を表す.
(1) 接線 \(\ell \) の傾きは
\begin{align}\left\{\left(~\fbox{$\hskip0.4emア\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~n+~\fbox{$\hskip0.4emイ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\right)e\right\}^{-~\fbox{$\hskip0.4emウ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}\end{align}
である.
(2)
\begin{align}I_n=\int_1^af_n(x)dx\end{align}
とすると
\begin{align} I_1=\frac{~\fbox{$\hskip0.4emエ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emオ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~},~I_{10}=\frac{\fbox{$\hskip0.4emカ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{~\fbox{$\hskip0.4emキク\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~-~\frac{\fbox{$\hskip0.4emケコ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{~\fbox{$\hskip0.4emサシス\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~e^{-~\frac{\fbox{$\hskip0.4emセ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{~\fbox{$\hskip0.4emソタ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}} \end{align}
である.
\(n=5\) とする. このとき\(,\) 曲線 \(C\) と接線 \(\ell\) および \(x\) 軸によって囲まれた領域(境界線を含む)を \(D\) とする.
(3) 領域 \(D\) の面積は
\begin{align}\frac{\fbox{$\hskip0.4emチ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{~\fbox{$\hskip0.4emツテ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~e^{-~\frac{~\fbox{$\hskip0.4emト\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emナ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}}~-\frac{\fbox{$\hskip0.4emニ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{~\fbox{$\hskip0.4emツテ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
である. また\(,\) 領域 \(D\) を \(x\) 軸のまわりに \(1\) 回転させてできる立体の体積は
\begin{align}\left(\frac{\fbox{$\hskip0.4emヌネ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{~\fbox{$\hskip0.4emノハヒ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~e^{-~\frac{~\fbox{$\hskip0.4emフ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emヘ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}}~-~\frac{\fbox{$\hskip0.4emホ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{~\fbox{$\hskip0.4emノハヒ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\right)~\pi \end{align}
である.
(1) の解答~接線の傾きは微分係数~
\begin{align}f_n^{\prime}(x)=-nx^{-n-1}\log{x}+x^{-n}\cdot \frac{1}{x}\end{align}
\begin{align}=x^{-n-1}(1-n\log{x})\end{align}
\begin{align}\ell ~:~y=a^{-n-1}(1-n\log{a})(x-a)+a^{-n}\log{a}\end{align}
\((0,~0)\) を通るので\(,\)
\begin{align}-a^{-n}(1-n\log{a})+a^{-n}\log{a}=0\end{align}
\(a^{-n}\neq 0\) より\(,\)
\begin{align}1-n\log{a}-\log{a}=0\end{align}
\begin{align}(n+1)\log{a}=1\end{align}
\(n\) は自然数であるから\(,\) \(n+1\neq 0\) なので
\begin{align}\log{a}=\frac{1}{n+1}\end{align}
\begin{align}a=e^{\frac{1}{n+1}}\end{align}
よって\(,\) \(\ell \) の傾きは
\begin{align}f_n^{\prime}\left(e^{\frac{1}{n+1}}\right)=e^{-1}\left(1-\frac{n}{n+1}\right)\end{align}
\begin{align}=\{(n+1)e\}^{-1}~~~~\cdots \fbox{答}\end{align}
ア:1 イ:1 ウ:1

quandle
アに \(1\) が入るとどきどきしてしまいますね笑
(2) の解答
\(I_1\) を求める~微分接触系は置換積分しない~
\begin{align}I_1=\int_1^{e^{\frac{1}{2}}}\frac{\log{x}}{x}dx\end{align}
\begin{align}=\biggl[\frac{1}{2}(\log{x})^2\biggr]_1^{e^{\frac{1}{2}}}=\frac{1}{8}~~~~\cdots \fbox{答}\end{align}
エ:1 オ:8

quandle
微分接触型になっているのに気付けましたか?
\begin{align}f(x)=x,~g(x)=\log{x}\end{align}
とおくと\(,\)
\begin{align}\frac{\log{x}}{x}=f(g(x))g^{\prime}(x)\end{align}
の形になっています. \(f(x)\) を積分したものに \(g(x)\) を代入するだけで置換積分せずに求めることができます!
\(I_{10}\) を求める~まずは一般項を求める~
\begin{align}I_n=\int_1^{e^{\frac{1}{n+1}}}x^{-n}\log{x}dx\end{align}
\begin{align}=\biggl[\frac{1}{1-n}x^{1-n}\log{x}\biggr]_1^{e^{\frac{1}{n+1}}}-\int_1^{e^{\frac{1}{n+1}}}\frac{1}{1-n}x^{1-n}\cdot \frac{1}{x}dx\end{align}
\begin{align}=\frac{1}{1-n^2}e^{\frac{1-n}{1+n}}-\frac{1}{(1-n)^2}\biggl[x^{1-n}\biggr]_1^{e^{\frac{1}{n+1}}}\end{align}
\begin{align}=\frac{1}{1-n^2}e^{\frac{1-n}{1+n}}-\frac{1}{(1-n)^2}\left(e^{\frac{1-n}{1+n}}-1\right)\end{align}
\begin{align}I_{10}=-\frac{1}{99}e^{-\frac{9}{11}}-\frac{1}{81}\left(e^{-\frac{9}{11}}-1\right)\end{align}
\begin{align}=\frac{1}{81}-\frac{20}{891}e^{-\frac{9}{11}}~~~~\cdots \fbox{答}\end{align}
カ:1 キ:8 ク:1 ケ:2 コ:0 サ:8 シ:9 ス:1 セ:9 ソ:1 タ:1
(3) の解答
\(D\) を図示する~\(\ell \) と \(y=f_5(x)\) の上下関係を把握する~
\begin{align}f_5(x)=x^{-5}\log{x}\end{align}
(1) より
\begin{align}f_5^{\prime}(x)=x^{-6}(1-5\log{x})\end{align}
増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|}\hline x & 0 & \cdots & \displaystyle e^{\frac{1}{5}} & \cdots \\ \hline f_5^{\prime}(x) & {} & + & 0 & – \\ \hline f_5(x) & {} & \nearrow & \displaystyle \frac{1}{5e} & \searrow \\ \hline \end{array}\end{align}
\begin{align}\lim_{x\to +0}\frac{\log{x}}{x^5}=-\infty ,~\lim_{x\to \infty}\frac{\log{x}}{x^5}=0\end{align}

quandle
\(x\to +0\) のときは不定形ではないので直ちに極限がわかります.
\(x\to \infty\) のときは \(\displaystyle \frac{\infty}{\infty}\) の不定形となってしまいます. こういうときは発散のスピードを考えればよく\(,\) \(x\to \infty\) のとき \(\log{x}<<x^5\) なので分母の発散のスピードのほうが分子の発散のスピードよりも遥かに速いため極限値は \(0\) であると判断ができます.
(1) より\(,\)
\begin{align}\ell ~:~y=\frac{1}{6e}x\end{align}
であり\(,\) 接点の座標は \(\displaystyle \left(e^{\frac{1}{6}},~\frac{1}{6e^{\frac{5}{6}}}\right)\) であるから\(,\) 領域 \(D\) は以下の青色部分となる.
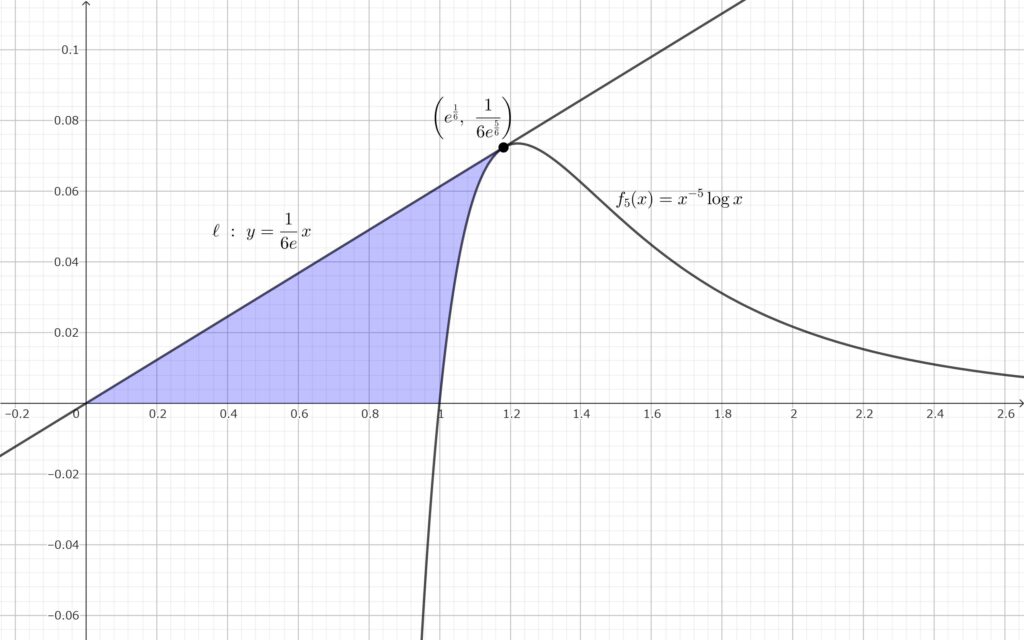
\(S\) を求める~三角形からくりぬく~
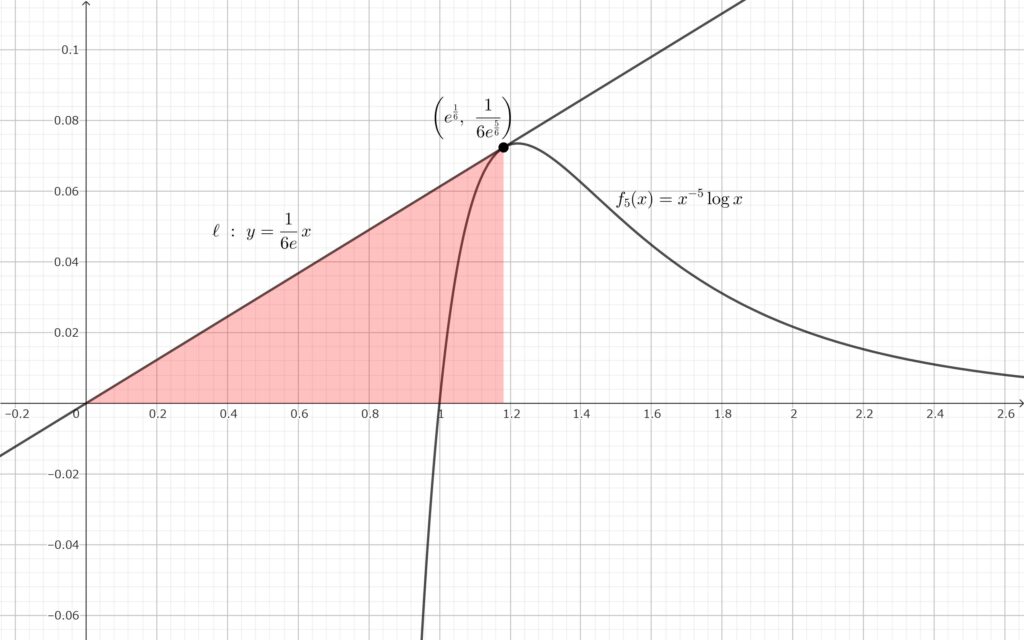
青色部分の面積は下図の赤色部分の面積から緑色部分の面積を引けばよい.

quandle
赤色部分は直角三角形なので積分せずに求められますね.
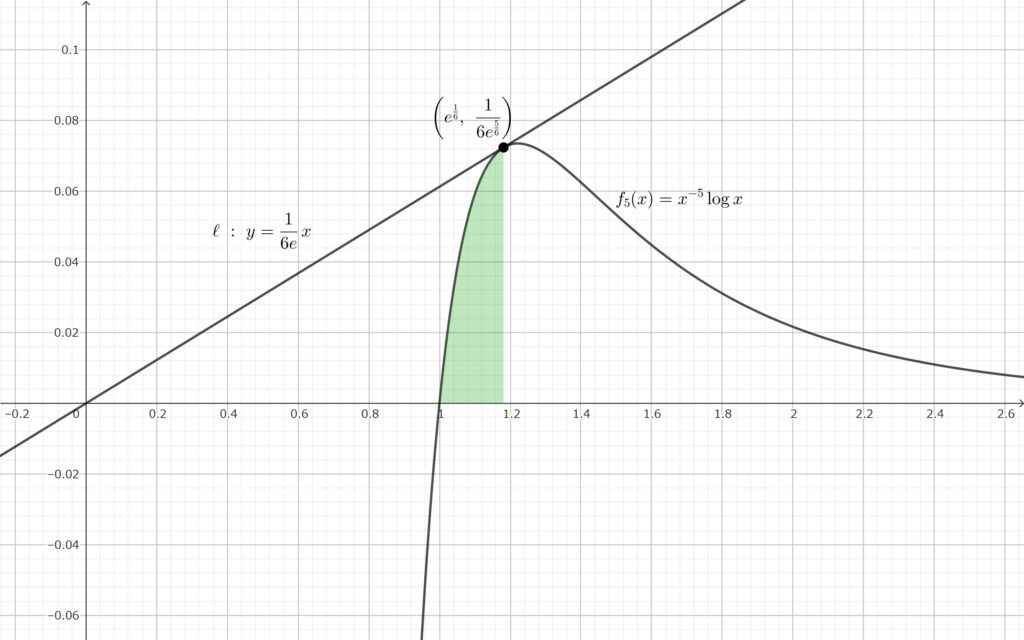
緑色部分は \(I_5\) そのものです. (2) で一般項を求めているので \(n=5\) を代入するだけで求められそうです.
(2) より\(,\)
\begin{align}I_5=\frac{1}{-24}e^{-\frac{2}{3}}-\frac{1}{16}\left(e^{-\frac{2}{3}}-1\right)\end{align}
\begin{align}=\frac{1}{16}-\frac{5}{48}e^{-\frac{2}{3}}\end{align}
であるから\(,\)
\begin{align}S=\frac{1}{2}\cdot e^{\frac{1}{6}}\cdot \frac{1}{6e^{\frac{5}{6}}}-I_5\end{align}
\begin{align}=\frac{1}{12}e^{-\frac{2}{3}}-\left(\frac{1}{16}-\frac{5}{48}e^{-\frac{2}{3}}\right)\end{align}
\begin{align}=\frac{3}{16}e^{-\frac{2}{3}}-\frac{1}{16}~~~~\cdots \fbox{答}\end{align}
チ:3 ツ:1 テ:6 ト:2 ナ:3 ニ:1
\(V\) を求める~円錐からくりぬく~
\(D\) を \(x\) 軸のまわりに \(1\) 回転してできる立体の体積は\(,\) 赤色部分を \(x\) 軸のまわりに \(1\) 回転してできる立体の体積から\(,\) 緑色部分を \(x\) 軸のまわりに \(1\) 回転させてできる立体の体積を引けばよい.

quandle
赤色部分を \(x\) 軸のまわりに \(1\) 回転させると円錐ができます. 円錐は体積公式を使うことで積分せずにすみます. 緑色部分を \(x\) 軸のまわりに \(1\) 回転させてできる立体の体積は頑張って部分積分をする必要がありそうです. 残念ながら \(I_n\) が使えそうにないですね.
\begin{align}V=\frac{1}{3}\cdot \left(\frac{1}{6e^{\frac{5}{6}}}\right)^2\pi \cdot e^{\frac{1}{6}}-\pi \int_1^{e^{\frac{1}{6}}}x^{-10}(\log{x})^2dx\end{align}
\begin{align}=\left\{\frac{1}{108}e^{-\frac{3}{2}}-\int_1^{e^{\frac{1}{6}}}x^{-10}(\log{x})^2dx\right\}\pi\end{align}
ここで\(,\)
\begin{align}\int_1^{e^{\frac{1}{6}}}x^{-10}(\log{x})^2dx\end{align}
\begin{align}=\biggl[-\frac{1}{9}x^{-9}(\log{x})^2\biggr]_1^{e^{\frac{1}{6}}}+\int_1^{e^{\frac{1}{6}}}\left\{\frac{1}{9}x^{-9}\cdot 2(\log{x})\cdot \frac{1}{x}\right\}dx\end{align}
\begin{align}=-\frac{1}{324}e^{-\frac{3}{2}}+\frac{2}{9}\int_1^{e^{\frac{1}{6}}}x^{-10}\log{x}dx\end{align}
であり\(,\)
\begin{align}\int_1^{e^{\frac{1}{6}}}x^{-10}\log{x}dx\end{align}
\begin{align}=\biggl[-\frac{1}{9}x^{-9}\log{x}\biggr]_1^{e^{\frac{1}{6}}}+\int_1^{e^{\frac{1}{6}}}\frac{1}{9}x^{-9}\cdot \frac{1}{x}dx\end{align}
\begin{align}=-\frac{1}{54}e^{-\frac{3}{2}}+\frac{1}{9}\biggl[-\frac{1}{9}x^{-9}\biggr]_1^{e^{\frac{1}{6}}}\end{align}
\begin{align}=-\frac{5}{162}e^{-\frac{3}{2}}+\frac{1}{81}\end{align}
であるから\(,\)
\begin{align}\int_1^{e^{\frac{1}{6}}}x^{-10}(\log{x})^2dx\end{align}
\begin{align}=-\frac{1}{324}e^{-\frac{3}{2}}+\frac{2}{9}\left(-\frac{5}{162}e^{-\frac{3}{2}}+\frac{1}{81}\right)\end{align}
\begin{align}=-\frac{29}{2916}e^{-\frac{3}{2}}+\frac{2}{729}\end{align}
以上より\(,\)
\begin{align}V=\left\{\frac{1}{108}e^{-\frac{3}{2}}-\left(-\frac{29}{2916}e^{-\frac{3}{2}}+\frac{2}{729}\right)\right\}\pi\end{align}
\begin{align}=\left(\frac{14}{729}e^{-\frac{3}{2}}-\frac{2}{729}\right)\pi ~~~~\cdots \fbox{答}\end{align}
ヌ:1 ネ:4 ノ:7 ハ:2 ヒ:9 フ:3 へ:2 ホ:2










コメント