問題文全文
放物線 \(D~:~y=x^2\) と\(,\) \(D\) 上を動く点 \(\mathrm{A}(a,~a^2)\) を考える. ただし\(,\) 以下では \(a\) は常に
\begin{align}0<a<1\end{align}
の範囲を動くとする.
点 \(\mathrm{A}\) における \(D\) の法線と \(D\) の交点のうち\(,\) \(\mathrm{A}\) 以外の点を \(\mathrm{B}(b,~b^2)\) とおく.
(1) \(b\) を \(a\) を用いて表せ. また\(,\) \(b\) のとり得る値の範囲を求めよ.
点 \(\mathrm{A}\) における \(D\) の接線と\(,\) 点 \(\mathrm{B}\) における \(D\) の接線の交点を \(\mathrm{P}\) とおく.
(2) 点 \(\mathrm{P}\) の座標を \(a\) を用いて表せ.
(3) \(\triangle \mathrm{ABP}\) の面積を \(S\) とおく. \(S\) を \(a\) を用いて表せ. また\(,\) \(S\) の最小値を求めよ.
(4) 点 \(\mathrm{B}\) における \(D\) の法線と \(D\) の交点のうち\(,\) \(\mathrm{B}\) 以外の点を \(\mathrm{C}(c,~c^2)\) とおく. \(c\) のとり得る値の範囲を求めよ.
(1) の解答
\(y^{\prime}=2x\) より\(,\) 点 \(\mathrm{A}\) における法線は
\begin{align}y=-\frac{1}{2a}(x-a)+a^2\end{align}
点 \(\mathrm{B}\) の \(x\) 座標は
\begin{align}x^2=-\frac{1}{2a}x+a^2+\frac{1}{2}\end{align}
の解である.
\begin{align}x^2+\frac{1}{2a}x-a^2-\frac{1}{2}=0\end{align}

quandle
この \(2\) 次方程式の解は点 \(\mathrm{A}\) と点 \(\mathrm{B}\) の \(x\) 座標と一致するはずです. つまり点 \(\mathrm{A}\) の \(x\) 座標である \(x=a\) を解にもつことがすでにわかっています. \(x-a\) で割り切れるはずですね.
\begin{align}(x-a)\left(x+\frac{1}{2a}+a\right)=0\end{align}
これが
\begin{align}(x-a)(x-b)=0\end{align}
と一致するので\(,\)
\begin{align}b=-a-\frac{1}{2a}~~~~\cdots \fbox{答}\end{align}
\(\displaystyle a>0,~\frac{1}{2a}\) であるから\(,\) 相加平均と相乗平均の関係より
\begin{align}b=-\left(a+\frac{1}{2a}\right)\leqq -2\sqrt{a\cdot \frac{1}{2a}}=-\sqrt{2}\end{align}
等号成立は
\begin{align}a=\frac{1}{2a}\end{align}
つまり
\begin{align}a=\frac{1}{\sqrt{2}}\end{align}
のときであり\(,\)
\begin{align}\lim_{a\to +0}\left(-a-\frac{1}{2a}\right)=-\infty\end{align}
であるから\(,\)
\begin{align}b\leqq -\sqrt{2}~~~~\cdots \fbox{答}\end{align}

quandle
\begin{align} \fbox{$\hskip0.5em\hskip0.5em\Rule{0pt}{0.5em}{0.4em}$} + \frac{定数}{\fbox{$\hskip0.5em\hskip0.5em\Rule{0pt}{0.5em}{0.4em}$}}\end{align}
の形を見たら相加平均と相乗平均の関係式がすぐに連想できるようにしておきたいです.
(2) の着眼点
放物線から引いた \(2\) 本の接線の交点の \(x\) 座標は\(,\) \(2\) つの接点の \(x\) 座標の平均になることが知られています. 入試では頻出なので結果を知っておきましょう. 詳しくは以下の記事にまとめていますのでご参照ください.
これを知っていれば求める交点 \(\mathrm{P}\) の \(x\) 座標は
\begin{align}\frac{a+b}{2}=\cfrac{a+\left(-a-\cfrac{1}{2a}\right)}{2}=-\frac{1}{4a}\end{align}
であることが予想できます.
今回は記述式ですから\(,\) きちんと求める過程を書く必要がありますが\(,\) 先に答えを知っておくことで見通しがよくなり\(,\) 安心して計算をすすめることができます.
(2) の解答
点 \(\mathrm{A}\)\(,\) 点 \(\mathrm{B}\) における \(D\) の接線はそれぞれ
\begin{align}y=2a(x-a)+a^2,~y=2b(x-b)+b^2\end{align}
であるから\(,\) 交点の \(x\) 座標は \(a\neq b\) であることに注意して\(,\)
\begin{align}2a(x-a)+a^2=2b(x-b)+b^2\end{align}
\begin{align}2(a-b)x=a^2-b^2\end{align}
\begin{align}x=\frac{a+b}{2}\end{align}
\begin{align}=\cfrac{a+\left(-a-\cfrac{1}{2a}\right)}{2}=-\frac{1}{4a}\end{align}
このとき\(,\) \(\mathrm{P}\) の \(y\) 座標は
\begin{align}y=2a\left(-\frac{1}{4a}-a\right)+a^2=-a^2-\frac{1}{2}\end{align}
\begin{align}\mathrm{P}\left(-\frac{1}{4a},~-a^2-\frac{1}{2}\right)~~~~\cdots \fbox{答}\end{align}
(3) の着眼点
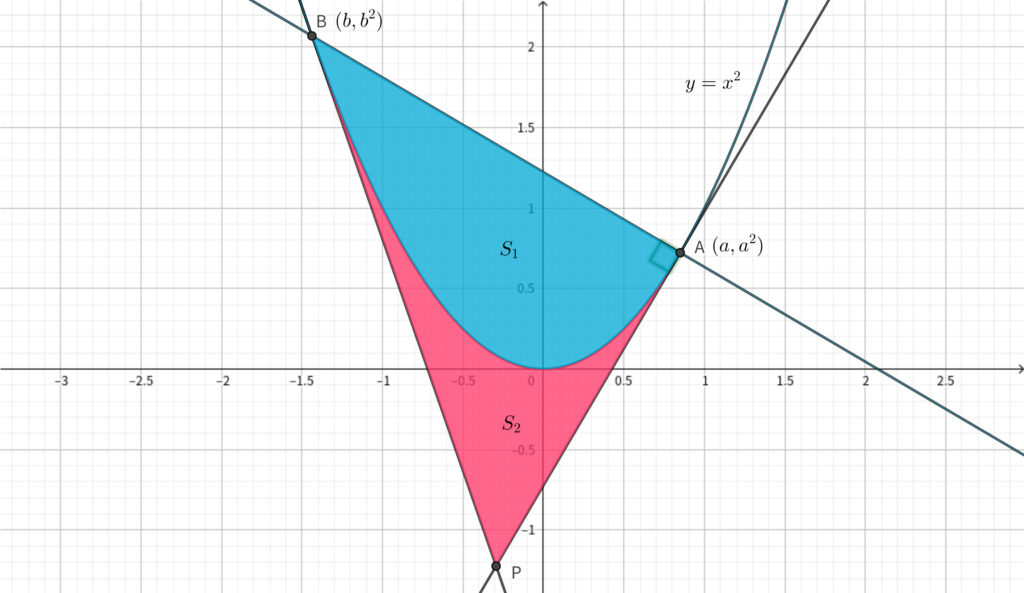
今回求めたい \(\triangle \mathrm{ABP}\) の面積は上図の \(S_1\) と \(S_2\) を足し合わせたものになります. \(S_1\) はいわゆる \(\frac{1}{6}\) 公式が使えますし\(,\) \(S_2\) は \(\frac{1}{12}\) 公式が使えます. (詳しくはこちら (2) と同じリンクです)
つまり\(,\)
\begin{align}S=S_1+S_2\end{align}
\begin{align}=\frac{1}{6}(a-b)^3+\frac{1}{12}(a-b)^3=\frac{1}{4}(a-b)^3\end{align}
\begin{align}=\frac{1}{4}\left(2a+\frac{1}{2a}\right)^3\end{align}
とかけることが予想できます. 今回は記述ですのでこの公式は使わずに計算しますが\(,\) 出てくる結果が最初からわかっているのはとても心強いです.
今回法線であることに注目すれば \(\triangle \mathrm{APB}\) が直角三角形であることが分かります.気付けていないと計算が大変だと思います.
(3) の解答
\begin{align}\mathrm{AB}=\sqrt{(b-a)^2+(b^2-a^2)^2}\end{align}
\begin{align}=\sqrt{\left(-2a-\frac{1}{2a}\right)^2+\left(\frac{1}{4a^2}+1\right)^2}\end{align}
\begin{align}=\sqrt{4a^2+\frac{1}{4a^2}+2+\frac{1}{16a^4}+\frac{1}{2a^2}+1}\end{align}
\begin{align}=\sqrt{4a^2+\frac{3}{4a^2}+\frac{1}{16a^4}+3}\end{align}
\begin{align}\mathrm{AP}=\sqrt{\left(\frac{b-a}{2}\right)^2+\left(-2a^2-\frac{1}{2}\right)^2}\end{align}
\begin{align}=\sqrt{\left(-a-\frac{1}{4a}\right)^2+\left(-2a^2-\frac{1}{2}\right)^2}\end{align}
\begin{align}=\sqrt{a^2+\frac{1}{16a^2}+\frac{1}{2}+4a^4+2a^2+\frac{1}{4}}\end{align}
\begin{align}=\sqrt{4a^4+3a^2+\frac{1}{16a^2}+\frac{3}{4}}\end{align}
よって\(,\)求める面積 \(S\) は
\begin{align}S=\frac{1}{2}\mathrm{AB}\cdot \mathrm{AP}\end{align}
\begin{align}=\frac{1}{2}\sqrt{4a^2+\frac{3}{4a^2}+\frac{1}{16a^4}+3}\sqrt{4a^2+3a^2+\frac{1}{16a^2}+\frac{3}{4}}\end{align}
\begin{align}=\frac{1}{2}\sqrt{16a^6+24a^4+15a^2+5+\frac{15}{16a^2}+\frac{3}{32a^4}+\frac{1}{256a^6}}\end{align}
\begin{align}=\frac{1}{2}\sqrt{\frac{1}{4}\left(64a^6+96a^4+60a^2+20+\frac{15}{4a^2}+\frac{3}{8a^4}+\frac{1}{64a^6}\right)}\end{align}
\begin{align}=\frac{1}{2}\sqrt{\frac{1}{4}\left\{(2a)^6+{}_6\mathrm{C}_1 (2a)^5\cdot \frac{1}{2a}+{}_6\mathrm{C}_2(2a)^4\cdot \left(\frac{1}{2a}\right)^2+{}_6\mathrm{C}_3(2a)^3\cdot \left(\frac{1}{2a}\right)^3+{}_6\mathrm{C}_4(2a)^2\cdot \left(\frac{1}{2a}\right)^4+{}_6\mathrm{C}_5\cdot 2a\cdot \left(\frac{1}{2a}\right)^5+\left(\frac{1}{2a}\right)^6\right\}}\end{align}
\begin{align}=\frac{1}{2}\sqrt{\frac{1}{4}\left(2a+\frac{1}{2a}\right)^6}=\frac{1}{4}\left(2a+\frac{1}{2a}\right)^3~~~~\cdots \fbox{答}\end{align}

quandle
答えの式があらかじめ分かっているからこそ6乗の展開に気付けます.
ここで\(,\) \(\displaystyle 2a>0,~\frac{1}{2a}>0\) であるから\(,\)
\begin{align}S=\frac{1}{4}\left(2a+\frac{1}{2a}\right)^3\end{align}
\begin{align}\geqq \frac{1}{4}\left(2\sqrt{2a\cdot \frac{1}{2a}}\right)^3=2\end{align}
等号成立は
\begin{align}2a=\frac{1}{2a}\end{align}
つまり
\begin{align}a=\frac{1}{2}\end{align}
のときである. よって\(,\)
\begin{align} S~の最小値は~2~~~~\cdots \fbox{答}\end{align}
(4) の解答
(1) と同様に
\begin{align}c=-b-\frac{1}{2b}=\frac{-2b^2-1}{2b}\end{align}
\begin{align}\frac{dc}{db}=\frac{-4b\cdot 2b-(-2b^2-1)\cdot 2}{4b^2}\end{align}
\begin{align}=\frac{-4b^2+2}{4b^2}<0~~(b\leqq \sqrt{2}より)\end{align}
であるから\(,\) \(c\) は \(b\leqq -\sqrt{2}\) において単調減少.
よって\(,\) \(b=-\sqrt{2}\) のとき \(c\) は最小値
\begin{align}c=\frac{-2(-\sqrt{2})^2-1}{2\cdot (-\sqrt{2})}=\frac{-5}{-2\sqrt{2}}=\frac{5\sqrt{2}}{4}\end{align}
をとり\(,\)
\begin{align}\lim_{b\to -\infty}\left(-b-\frac{1}{2b}\right)=\infty\end{align}
であるから\(,\) 求める \(c\) の範囲は
\begin{align}c\geqq \frac{5\sqrt{2}}{4}~~~~\cdots \fbox{答}\end{align}

quandle
\(c\) も相加平均と相乗平均の関係から範囲が出せそうですがなぜ使わなかったのか分かりますか? 等号成立条件である
\begin{align}-b=-\frac{1}{2b}\end{align}
を解いて出てくる \(\displaystyle b=-\frac{1}{\sqrt{2}}\) が残念ながら \(b\leqq -\sqrt{2}\) を満たしていないためです. もっと小さな数で評価できてしまう可能性が否定できなくなってしまうため\(,\) 相加平均と相乗平均の関係が使えません.
bとc の範囲のシミュレーション
\(\displaystyle b\leqq -\sqrt{2}\fallingdotseq -1.44,~c\geqq \frac{5\sqrt{2}}{4}\fallingdotseq 1.77\) であることを視覚的に理解できるシミュレーションを作りました. 点 \(\mathrm{A}\) の \(x\) 座標である \(a\) の値をスライダーを動かすことで\(,\) 点 \(\mathrm{B}\) の \(x\) 座標が青い点で\(,\) 点 \(\mathrm{C}\) の \(x\) 座標が赤い点で描かれます.










コメント