公立諏訪東京理科大学2023年推薦第3問の問題文全文
\(0<a<\sqrt{6}\) とし\(,\) 座標平面上の放物線 \(y=6-x^2\) と放物線上の点 \(\mathrm{A}(a,~6-a^2)\) を考える. \(\mathrm{A}\) を通り\(x\) 軸と平行な直線と放物線との交点で\(,\) \(\mathrm{A}\) とは異なる交点を \(\mathrm{B}\) とする. また\(,\) \(\mathrm{A}\) から \(x\) 軸に下した垂線と \(x\) 軸との交点を \(\mathrm{C}\) とし\(,\) \(\mathrm{B}\) から \(x\) 軸に下した垂線と \(x\) 軸の交点を \(\mathrm{D}\) とし\(,\) 長方形 \(\mathrm{ABDC}\) の面積 \(S\) とする. このとき\(,\) 以下の問いに答えよ.
(1) \(\mathrm{B}\) の座標を求めよ.
(2) \(S\) を \(a\) で表せ.
(3) \(S\) の最大値を求めよ.
(4) 放物線と線分 \(\mathrm{AB}\) で囲まれる面積を \(S_1\) とする. \(S_1\) が \(S\) と等しくなる \(a\) の値を求めよ.
(1) の解答〜 \(x\) 座標の符号を変えるだけ〜
\(\mathrm{B}\) は \(\mathrm{A}(a,~6-a^2)\) を \(y\) 軸に関して対称に移動した点であるから\(,\)
\begin{align}\mathrm{B}(-a,~6-a^2)~~~~\cdots \fbox{答}\end{align}
(2) の解答〜長方形の面積は縦×横〜
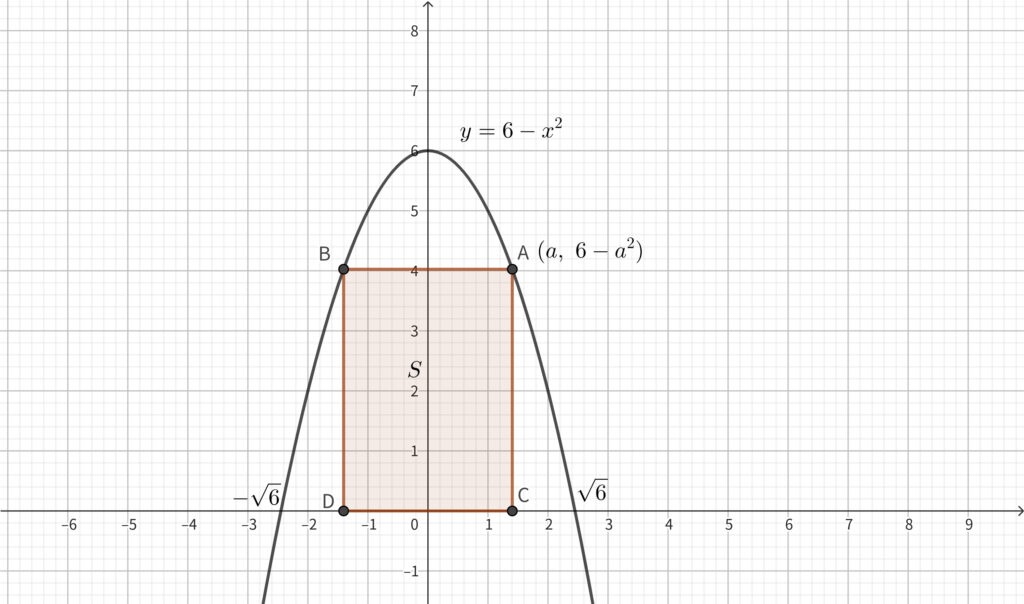
\begin{align}S=\mathrm{AB}\times \mathrm{AC}\end{align}
\begin{align}=2a(6-a^2)~~~~\cdots \fbox{答}\end{align}
(3) の解答〜3次関数の最大値は微分で求める〜
\begin{align}S=-2a^3+12a\end{align}
\begin{align}S^{\prime}=-6a^2+12=-6(a-\sqrt{2})(a+\sqrt{2})\end{align}
増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|}\hline a & 0 & \cdots & \sqrt{2} & \cdots & \sqrt{6} \\ \hline S^{\prime} & {} & + & 0 & – & {} \\ \hline S & 0 & \nearrow & 8\sqrt{2} & \searrow & 0 \\ \hline \end{array}\end{align}
増減表より\(,\)
\begin{align}a=\sqrt{2}~のとき最大値~8\sqrt{2}~~~~\cdots \fbox{答}\end{align}
(4) の解答〜\(\displaystyle \frac{1}{6}\) 公式の活用〜
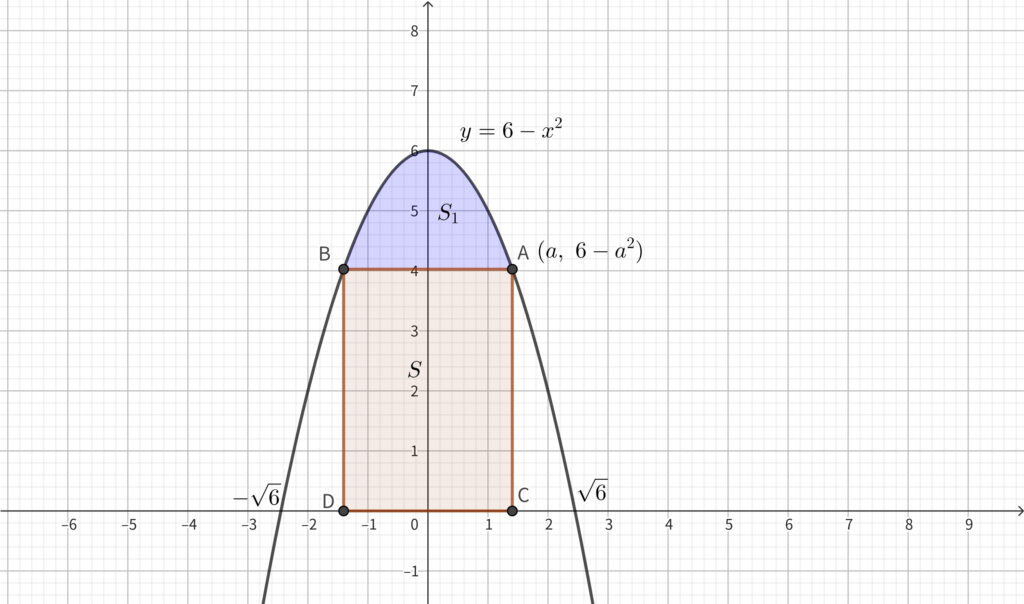
\(S_1\) を求めるときに \(\displaystyle \frac{1}{6}\) 公式を使うと早いです. 忘れた方は以下にまとめていますのでご覧ください.
\begin{align}S_1=\int_{-a}^a\{(6-x^2)-(6-a^2)\}dx\end{align}
\begin{align}=\int_{-a}^a-(x-a)(x+a)dx\end{align}
\begin{align}=\frac{1}{6}\{a-(-a)\}^3=\frac{4}{3}a^3\end{align}
\(S=S_1\) より\(,\)
\begin{align}-2a^3+12a=\frac{4}{3}a^3\end{align}
\begin{align}5a^3-18a=0\end{align}
\(a\neq 0\) より\(,\)
\begin{align}5a^2-18=0\end{align}
\(0<a<\sqrt{6}\) より\(,\)
\begin{align}a=\frac{3\sqrt{2}}{\sqrt{5}}=\frac{3\sqrt{10}}{5}~~~~\cdots \fbox{答}\end{align}

quandle
\begin{align}a=\frac{3\sqrt{10}}{5}=\sqrt{\frac{90}{25}}=\sqrt{3.6}<\sqrt{6}\end{align}
ですから\(,\) \(0<a<\sqrt{6}\) の範囲にありますね!








コメント