問題文全文
曲線 \(y=3x^2-10x+8~(t\leqq x \leqq t+1)\) および \(3\) 直線 \(y=x\)\(,\) \(x=t\)\(,\) \(x=t+1\) で囲まれる部分の面積を \(S(t)\) とするとき\(,\) 以下の問いに答えなさい.
(1) \(S(0)\) を求めなさい.
(2) \(S(t)~(0 \leqq t \leqq 1)\) を求めなさい.
(3) \(0 \leqq t \leqq 1\) における \(S(t)\) の最大値を求めなさい.
着眼点
① 積分を用いて面積を出す問題で何より大事なのは必ずしも正確な図である必要はないが\(,\)
上下関係と交点の座標はしっかり調べること
です. なぜなら
上下関係は被積分関数に\(,\) 交点の座標は積分区間
にそれぞれ対応するからです. 逆に言えば面積を求めるのに大事なのは上記 \(2\) つだけなので他の情報はないならないで問題ないということです.
今回で言えば放物線の頂点の座標は（あったほうがより正確なグラフがかけるけど）なくても問題を解く上では影響がありません.
② 定義域が \(t\leqq x \leqq t+1\) と文字で与えられています. \(t\) の値が変わると定義域が変わるので
もしかしたら \(t\) の値によって \(S(t)\) に場合分けが発生するかもしれません. \(t\) を動かしたときに \(S(t)\) のとり方が変わらないかに注目しながら問題を解きましょう. そのときに大事な観点は
幅は常に \(1\) である
ということです. 定義域は確かに動きますが幅は常に一定で変わることはありません.
グラフの概形について
\begin{align}3x^2-10x+8=x\end{align}
のとき\(,\)
\begin{align}3x^2-11x+8=0\end{align}
\begin{align}(x-1)(3x-8)=0\end{align}
\begin{align}x=1,~\frac{8}{3}\end{align}
\begin{align}3x^2-10x+8=0\end{align}
のとき\(,\)
\begin{align}(x-2)(3x-4)=0\end{align}
\begin{align}x=\frac{4}{3},~2\end{align}
よって\(,\) グラフの概形は以下のようになる.
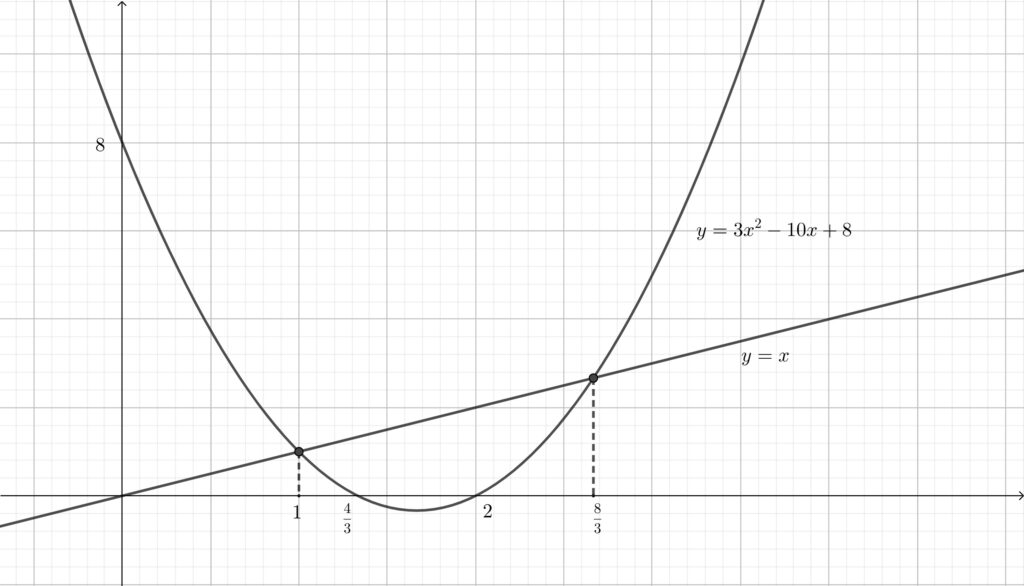※交点と上下関係さえわかればよいので極端に描いていますが実際はもっと細長くなります.
(1) の解答
\(t=0\) のとき\(,\) 曲線 \(y=3x^2-10x+8\) と \(3\) 直線 \(y=x\)\(,\) \(x=0\)\(,\) \(x=1\) で囲まれた部分は以下の図の青色部分であるから\(,\)
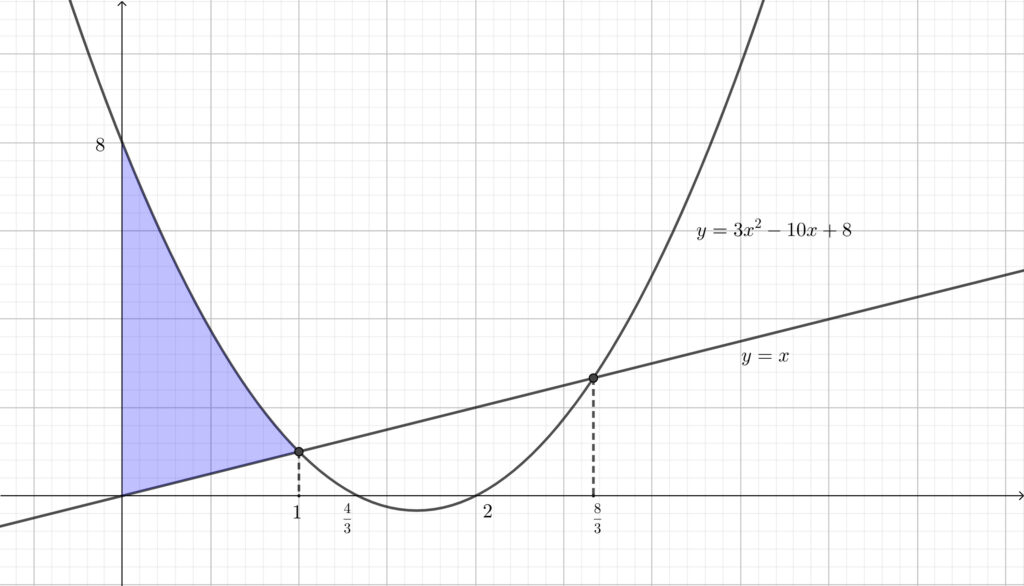
\begin{align}S(0)=\int_0^1\{(3x^2-10x+8)-x\}dx\end{align}
\begin{align}=\biggl[x^3-\frac{11}{2}x^2+8x\biggr]_0^1\end{align}
\begin{align}=1-\frac{11}{2}+8=\frac{7}{2}~~~~\cdots \fbox{答}\end{align}
(2) の解答
\begin{align}f(x)=(3x^2-10x+8)-x=3x^2-11x+8\end{align}
\begin{align}F(x)=\int f(x) dx=x^3-\frac{11}{2}x^2+8x+C\end{align}
とおく.
quandle
\(t=1\) のとき\(,\) 曲線 \(y=3x^2=10x+8\) と \(3\) 直線 \(y=x\)\(,\) \(x=1\)\(,\) \(x=2\) で囲まれる部分は下図の緑色部分であるから\(,\)
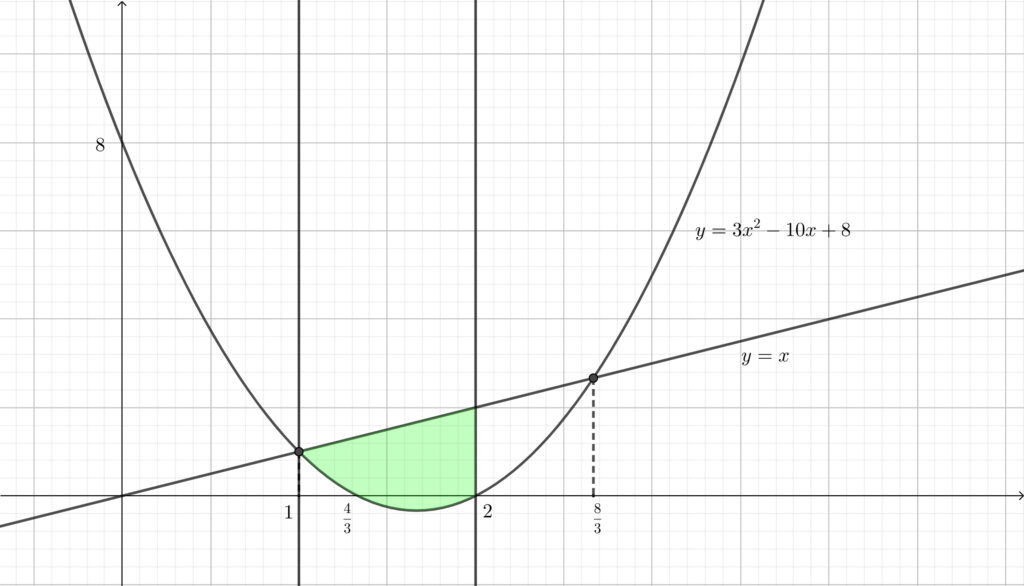
\begin{align}S(1)=\int_1^2\{x-(3x^2-10x+8)\}dx\end{align}
\begin{align}=\biggl[-F(x)\biggr]_1^2=-F(2)+F(1)\end{align}
\begin{align}=-(8-22+16)+\frac{7}{2}=\frac{3}{2}\end{align}
quandle
\(F(1)\) は (1) ですでに計算済みで \(\displaystyle \frac{7}{2}\) とわかってますね.
\(0<t<1\) のとき\(,\) 曲線 \(y=3x^2-10x+8\) と \(3\) 直線 \(y=x\)\(,\) \(x=t\)\(,\) \(x=t+1\) で囲まれた部分は以下の図の赤色部分であるから\(,\)
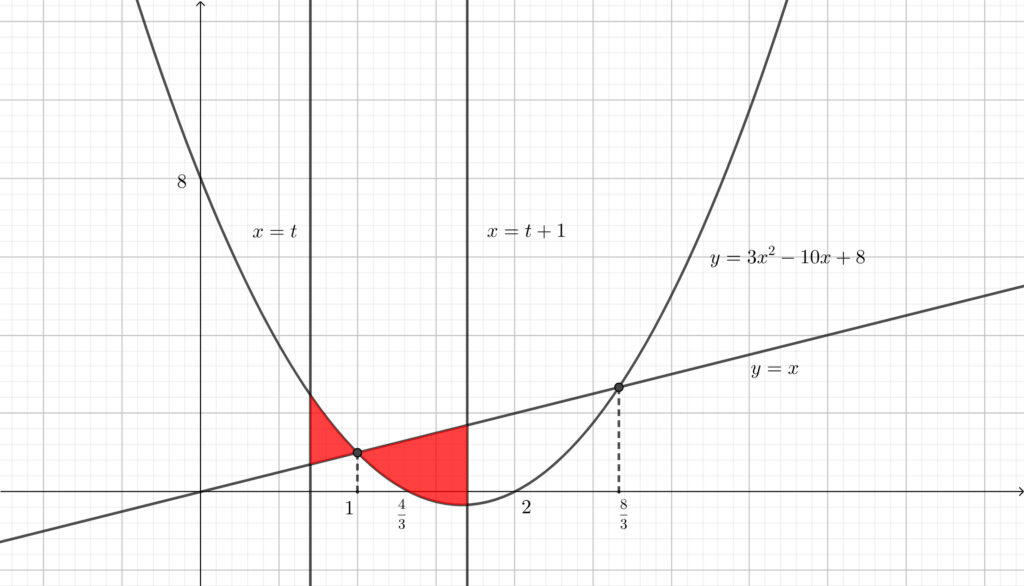
\begin{align}S(t)=\int_t^1f(x)dx+\int_1^{t+1}-f(x)dx\end{align}
\begin{align}=\biggl[F(x)\biggr]_t^1-\biggl[F(x)\biggr]_1^{t+1}=F(1)-F(t)-\{F(t+1)-F(1)\}\end{align}
\begin{align}=2F(1)-\{F(t)+F(t+1)\}\end{align}
\begin{align}=2\cdot \frac{7}{2}-\left\{t^3-\frac{11}{2}t^2+8t+(t+1)^3-\frac{11}{2}(t+1)^2+8(t+1)\right\}\end{align}
\begin{align}=7-\left(2t^3-8t^2+8t+\frac{7}{2}\right)=-2t^3+8t^2-8t+\frac{7}{2}\end{align}
\(t=0\) のとき\(,\) \(\displaystyle \frac{7}{2}\) となり\(,\) \(S(0)\) に一致し\(,\)
\(t=1\) のとき\(,\) \(\displaystyle -2+8-8+\frac{7}{2}=\frac{3}{2}\) となり\(,\) \(S(1)\) に一致するので\(,\)
\(0 \leqq t \leqq 1\) において\(,\)
\begin{align}S(t)=-2t^3+8t^2-8t+\frac{7}{2}~~~~\cdots \fbox{答}\end{align}
quandle
本解答ではかなり丁寧に
\begin{align}t=0,~0<t<1,~t=1\end{align}
の \(3\) つに場合分けしてそれらが一致することを示しました.
実際の試験では最初から \(0\leqq t \leqq 1\) として 赤色部分の計算をして \(S(t)\) としても減点はされないと思います. （あくまで個人の感想です）
(3) の解答
\begin{align}S^{\prime}(t)=-6t^2+16t-8=-2(t-2)(3t-2)\end{align}
\(S^{\prime}(t)=0\) のとき\(,\) \(\displaystyle t=\frac{2}{3},~2\) より\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|}\hline t & 0 & \cdots & \displaystyle \frac{2}{3} & \cdots & 1 \\ \hline S^{\prime}(t) & {} & – & 0 & + & {} \\ \hline S(t) & {} & \searrow & 極小 & \nearrow & {} \\ \hline \end{array}\end{align}
増減表より\(,\) \(\displaystyle t=\frac{2}{3}\) のとき最小値
\begin{align}S\left(\frac{2}{3}\right)=-2\cdot \frac{8}{27}+8\cdot \frac{4}{9}-8\cdot \frac{2}{3}+\frac{7}{2}\end{align}
\begin{align}=\frac{-32+192-288+189}{54}=\frac{61}{54}~~~~\cdots \fbox{答}\end{align}
コメント